 |
3.2. Механическая работа. Мощность.
|
|
|
|
3. 2. Механическая работа. Мощность.
Консервативные и диссипативные силы
Если под действием силы тело перемещается, то совершается механическая работа.
|
Рис. 3. 2 |
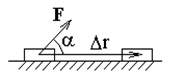
Механическая работа, совершаемая постоянной силой 
при прямолинейном перемещении тела D 
, равна произведению модуля вектора силы на модуль
вектора перемещения и косинус угла между направлениями силы и перемещения (рис. 3. 2)
A = FDrcosa. (3. 6)
Введем обозначение
Ft = Fcosa.
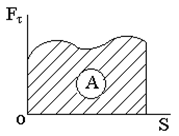
Пусть график Ft = f(S) имеет вид (рис. 3. 3).
В координатах Ft(S) площадь под графиком Ft = f(S) численно равна работе.
Быстрота совершения работы характеризуется мощностью
N = A/t.
|
Рис. 3. 3 |
Мощность силы (мощность) равна отношению работы силы, совершенной за время t, к этому промежутку времени.
Для равномерного прямолинейного движения значение мощности рассчитывается по формуле
( , 
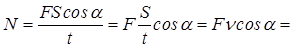), (3. 10)
где - скорость тела.
Для неравномерного движения средняя мощность < N > и мгновенная мощность N определяются выражениями
< N > = F< n > cosa; N = Fncosa, (3. 11)
| 
| 
|
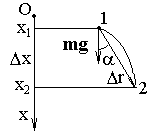
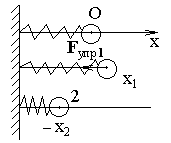
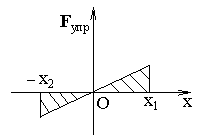
| Рис. 3. 4 | Рис. 3. 5 | Рис. 3. 8 |
где < n > - величина средней скорости, n - величина мгновенной скорости тела.
Система тел, в которой действуют только консервативные силы, называется консервативной.
Силы, работа которых по замкнутой траектории равна нулю, называются консервативными или потенциальными. К ним относятся силы гравитационного взаимодействия, упругости, кулоновские, архимедовы силы и т. д.
Силы, работа которых по замкнутой траектории не равна нулю, называются неконсервативными или диссипативными.
К ним относятся силы трения, сопротивления среды и т. д.
Работа силы тяжести. В однородном поле тяжести (g = const) при перемещении материальной точки из положения 1 в положение 2 (рис. 3. 4) по любой траектории для работы силы тяжести m 
получим
|
|
|
A(mg) = mgDrcosa = mgDx, (3. 8)
где Dx - проекция перемещения Dr на ось ОХ.
Работа силы упругости пружины.
Пружину растянули на х1, а затем груз отпустили (рис. 3. 5). Работа силы упругости при перемещении груза из положения 1 в положение 2, равна
А(Fупр) = (1/2)к(х12 - х22). (3. 9)
3. 3. Энергия. Кинетическая и потенциальная энергия.
Теорема об изменении кинетической энергии
Энергия - универсальная количественная мера всех форм движения и взаимодействия материи.
Механическая энергия - скалярная функция состояния системы тел, характеризующая способность системы совершать механическую работу.
Кинетической энергией называется энергия, которой обладает тело вследствие своего движения.
Тело массой m, движущееся со скоростью n, обладает кинетической энергией
Wк = mn2/2. (3. 10)
Теорема об изменении кинетической энергии: изменение кинетической энергии тела равно работе всех сил, действующих на тело
DWк = А (всех сил). (3. 11)
Потенциальной энергией называется энергия, которая определяется взаимным положением тел или частей тела, между которыми действуют потенциальные силы.
Потенциальная энергия тела в поле тяжести Земли
Wп = mgh, (3. 12)
где h - высота подъема тела над уровнем, на котором потенциальная энергия тела принята равной нулю.
Потенциальная энергия упруго деформированного тела (пружины)
Wп = кх2/2,
где к - коэффициент жесткости, х - величина деформации.
За нулевой уровень потенциальной энергии пружины принято состояние при х = 0, т. е. пружина не деформирована.
|
|
|
Изменение потенциальной энергии системы тел (тела) равно работе потенциальных сил, взятой с обратным знаком
DWп = - А (потенц. сил).
Полная механическая энергия системы
W = Wк + Wп.
Закон сохранения механической энергии: полная механическая энергия замкнутой и консервативной системы тел с течением времени не изменяется
W = const.
Если система не замкнута и не консервативна (действуют диссипативные силы), то изменение механической энергии системы тел равно работе внешних сил и внутренних неконсервативных сил
DW = А (внеш. ) + А (внутр. неконс. ).
Закон сохранения механической энергии есть частный случай закона сохранения энергии, который является фундаментальным законом природы: энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой в равных количествах.
|
|
|
