 |
2.6. Криволинейное движение. Ускорение свободного падения.
|
|
|
|
2. 6. Криволинейное движение. Ускорение свободного падения.
Основное уравнение динамики материальной точки применимо к движению по любой траектории.
Составляя уравнение движения материальной точки по окружности, нужно помнить, что в этом случае ускорение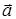 
может быть разложено на нормальную 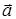n и касательную 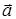t составляющие, т. е.
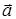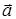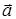= n + t.
В соответствии с этим направление координатных осей ОХ и ОY, на которые проецируется основное уравнение динамики материальной точки, выбираются по нормали (к центру) и касательной к окружности.
Формула для вычисления нормального (центростремительного) ускорения
аn = 
,
где R - радиус кривизны траектории.
Ускорение свободного падения g, сообщаемое телу Землей, на расстоянии r от центра (r ³ R, R - радиус Земли)
g = G 
,
где М - масса Земли.
Ускорение свободного падения на поверхности Земли
g0 = G = 9, 8 м/с2.
Ускорение свободного падения g на высоте h над поверхностью Земли
g = 
.
2. 7. Общая формулировка второго закона Ньютона
Импульсом тела (материальной точки) называется векторная величина 
, равная произведению массы m тела на его скорость 
(рис. 2. 8)
= m .
|
Рис. 2. 8 |
Пользуясь понятием импульса, второй закон Ньютона можно записать так
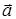= m = mD /Dt = D(m )/Dt.
Если на тело действует сила в течение времени Dt, то импульс тела изменяется на величину D(m ) = Dt
D = Dt.
Произведение силы на время ее действия Dt называют импульсом силы.
Более общая формулировка второго закона Ньютона: изменение импульса тела равно импульсу действующей на него силы.
III. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
3. 1. Импульс системы материальных точек.
Закон сохранения импульса
|
|
|
Рассмотрим систему, состоящую из двух материальных точек, массы и скорости которых соответственно равны m1, m2 и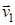 
, 
.
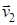Силы взаимодействия между материальными точками системы называют внутренними.
Силы, с которыми на материальные точки системы действуют внешние объекты, называют внешними.
Импульс системы материальных точек равен векторной сумме импульсов отдельных точек в один и тот же момент времени
= m1 
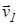+ m2 
= 
.
Изменение импульса системы частиц равно импульсу всех внешних сил, действующих на эту систему.
D = Dt, (3. 1)
где = 1 + 2 - векторная сумма внешних сил, действующих на рассматриваемую систему тел.
Система материальных точек, на которую не действуют внешние силы, называется замкнутой.
В замкнутой системе
D / Dt = 0.
Следовательно,
= 
= const. (3. 2)
Это закон сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Закон сохранения импульса можно применить, строго говоря, только к замкнутым системам, т. е. к таким системам тел, на каждое из которых не действуют внешние силы или векторная сумма внешних сил равна нулю
= 0. (3. 3)
Если система не замкнута, т. е. равнодействующая внешних сил не равна нулю
¹ 0,
но проекция равнодействующей внешних сил на некоторое направление во время взаимодействия равна нулю
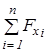=0,
то сохраняется проекция импульса системы на это направление
Рх =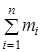 
nхi= const. (3. 4)
Систему можно считать замкнутой в течение такого малого промежутка времени, на протяжении которого в системе возникают внутренние силы взаимодействия, во много раз превосходящие внешние силы. И тогда импульс системы остается постоянным
|
|
|
1 = 2. (3. 5)
Эти условия выполняются при ударах и взрывах. 
|
|
|
