 |
Теоретическое ввдение. Кинематика материальной точки. 1. 2. Основные понятия кинематики. 1. 3. Скорость. 1. 4. Ускорение
|
|
|
|
Теоретическое ввдение
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ
1. 2. Основные понятия кинематики
Кинематика - раздел механики, изучающий движение тел, не рассматривая причин, которые это движение обусловливают.
Механическое движение - это изменение положения тела в пространстве относительно других тел с течением времени.
Материальной точкой называется тело, форма и размеры которого несущественны в данной задаче.
Тело, условно принимаемое за неподвижное, относительно которого рассматривается движение других тел, называется телом отсчета.
Система отсчета - это совокупность системы координат и часов, связанных с телом отсчета.
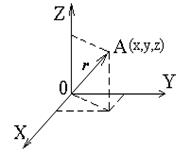
В трехмерном пространстве положение материальной точки А в декартовой системе координат определяется в данный момент времени тремя координатами х, у, z или радиусом - вектором 
, проведенным из начала системы координат в данную точку (рис. 1. 8).
|
Рис. 1. 8 |
При движении материальной точки ее радиус - вектор и координаты изменяются с течением времени.
В общем случае ее движение определяется векторным уравнением
= ( t ), (1. 3)
или скалярными уравнениями
(1. 4)
Уравнения (1. 3) и (1. 4) называются кинематическими уравнениями движения точки.
|
Рис. 1. 9 |
Траекторией называется линия, которую описывает материальная точка при движении относительно выбранной системы отсчета.
Длина участка траектории, пройденного точкой при ее движении, называется пройденным путем S (рис. 1. 9).
Вектором перемещения D называется вектор, проведенный из начального положения движущейся точки в конечное положение
|
|
|
D = - 0.
1. 3. Скорость
Для характеристики направления и быстроты движения материальной точки вводится векторная величина - скорость.
Вектором средней скорости < 
> называется отношение вектора перемещения к промежутку времени, за который это перемещение произошло (рис. 1. 13)
< > = D /Dt.
Скоростью точки в момент времени t называется вектор , равный первой производной по времени от радиуса - вектора этой точки
= 
.
Вектор скорости направлен по касательной к траектории точки в сторону ее движения (рис. 1. 10).
Проекции скорости на оси координат vх и vу равны производным соответственно от координат х и у по времени t
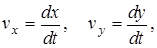
При равномерном движении точки остается постоянным модуль скорости
|
Рис. 1. 10 |
v= const.
Кинематическое уравнение равномерного движения в векторном виде
= 0 + t,
где 0 - начальный радиус - вектор, определяющий положение точки в момент времени t0 = 0, - начальная скорость.
Если движение неравномерное, то вводят понятие средней скорости ( 
- скаляр) на пути S за данный промежуток времени t
1. 4. Ускорение
Для характеристики быстроты изменения скорости точки по модулю и направлению служит векторная величина - ускорение.
|
|
Средним ускорением неравномерного движения называется векторная величина, равная отношению изменения вектора скорости к промежутку времени, за который произошло это изменение
=D /Dt.
Мгновенным ускорением (ускорением) точки в момент времени t называется векторная величина, равная первой производной скорости по времени
В случае произвольного криволинейного движения вектор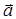 
направлен под некоторым углом a к вектору (рис. 1. 11).
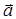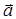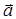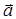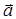Удобно вектор ускорения разложить на две составляющие t и n, направленные по касательной к траектории (t) и нормали (n), т. е. = t + n.
|
|
|
Составляющая 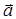t называемая тангенциальным (касательным) ускорением точки, характеризует быстроту изменения модуля ее скорости
аt =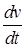 
.
Составляющая 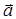n называется нормальным ускорением точки. Она характеризует быстроту изменения направления вектора скорости точки
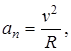
где R - радиус кривизны траектории в данной точке.
Движение точки называется равнопеременным, если тангенциальное ускорение аt = const.
Кинематические векторные уравнения равнопеременного движения имеют вид
где 0 - начальный радиус - вектор, определяющий положение тела в начальный момент t0 = 0; 0 - начальная скорость тела, 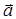- ускорение.
|
|
|
