IV. Статика твердого тела. 4. 1. Условия равновесия. Момент силы . Относительно оси вращения. V. Динамика твёрдого тела. 1. Момент инерции твёрдого тела.

IV. Статика твердого тела

4. 1. Условия равновесия. Момент силы 

относительно оси вращения

Статика - раздел механики, изучающий условия равновесия тела или системы тел под действием сил.

Условие равновесия поступательно движущегося тела

 (материальной точки)

Чтобы материальная точка находилась в равновесии, необходимо, чтобы векторная сумма всех сил, приложенных к ней, была равна нулю (первое условие равновесия)

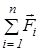= 0.

Условие равновесия тела с закрепленной осью

Рассмотрим новую величину - момент силы относительно оси вращения.

Моментом силы  относительно оси вращения называется векторная величина, равная векторному произведению радиуса - вектора  и вектора силы  (рис. 4. 1)

Модуль момента силы равен

М = Frsina = Fd,

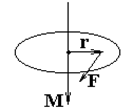Рис. 4. 1

Рис. 4. 2

где F - модуль силы, d = rsina - плечо силы (кратчайшее расстояние от оси вращения до линии действия силы) (рис. 4. 2).

Тело, способное вращаться вокруг закрепленной оси, находится в равновесии, если векторная сумма моментов всех сил относительно этой оси равна нулю (второе условие равновесия)

= 0.

Сформулируем общие условия равновесия твердого тела: для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма всех сил, приложенных к телу равнялась нулю и, чтобы векторная сумма моментов всех сил относительно оси вращения равнялась нулю

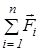= 0,                                              (4. 1)

= 0.                                            (4. 2)

Важное понятие статики - центр тяжести тела.

Центром тяжести тела или системы тел называют точку, относительно которой векторная сумма моментов сил тяжести всех частиц тела или системы тел равна нулю.

Определим центр тяжести системы трех материальных точек m₁, m₂, m₃, расположенных вдоль оси ОХ. Пусть координаты точек на этой оси равны х₁, х₂, х₃; х_с - координата центра тяжести системы (рис. 4. 3), которую можно рассчитать по формуле:

 

Рис. 4. 3

 

х_с = .

При определении положения центра тяжести тел сложной конфигурации необходимо учитывать, что:

а) центр тяжести симметричных тел лежит на оси симметрии,

б) можно представить тело сложной формы как систему тел простой формы.

V. ДИНАМИКА ТВЁРДОГО ТЕЛА.

 

Абсолютно твердым телом называют абсолютно неизменяемую сис­тему точек, отдельных частиц тела, поэтому к абсолютно твердому телу можно применить уже описанные законы динамики системы точек при условии ее неизменяемости.

1. Момент инерции твёрдого тела.

Для описания вращательного движения тела существенно значение его момента инерции. По определению момент инерции твердого тела относительно оси равен сумме моментов инерции отдельных его частиц:

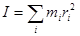
где 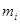- масса -й частицы тела,  - ее расстояние частицы до оси.

 

 

2. Примеры расчёта моментов инерции.

2. 1. Момент инерции тонкого стержня относительно оси, перпендикулярной стержню

 и проходящий через его центр масс.

Если стержень имеет массу   и длину 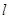, а ось  проходит через центр масс стержня (рис. ), то коор­динаты левого и правого концов стерж­ня равны -   и 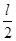. Выделим в стержне на расстоянии   от оси малый его участок длины 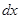. Его мо­мент инерции относительно  равен:

                                                      

Интегрируя, получим:

                                      

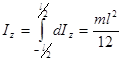
2. 2. Момент инерции тонкой пластины прямоугольной формы относительно

 одной из её сторон.

 

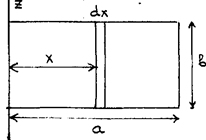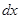Размеры тонкой пластины массы  приведены на рис., выделим в пластине на расстоянии  от оси   узкий слой ширины  и запишем его момент инер­ции:

                                    

Интегрируя (258), получаем:

                                                          

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: