 |
§3. Работа и мощность. Работа постоянной силы
|
|
|
|
§3. Работа и мощность. Работа постоянной силы
Работой силы называют меру действия силы, зависящую от ее модуля и
направления и от перемещения точки приложения сил ы.
Работа постоянной силы по определению равна скалярному произвед е-
нию силы на перемещение . Это определение работы проиллюстрировано
на рис. 5. 4 и записано в виде формулы (5. 3).
Рис. 5. 4
. (5. 3) Из формулы (5. 3) следует, что в зависимости от направления силы работа
мо жет быть положительной (если cos > 0), отрицательной (если cos < 0)
и равной нулю (если cos = 0 при = 90 ). Физический смысл понятия «раб о-
та» в механике Ньютона выясняется при введении понятий кинетической и п о-
тенциальной эне ргии материальной точки.
Элементарная работа
В случае, если сила не является постоянной, формулу (5. 3) можно испол ь-
зовать для нахождения элементарной работы, сов ершаемой при бесконечно м а-
лом перемещении, так как при этом силу можно считать постоянной. Рис.
5. 5 иллюстрирует формулу (5. 4) для элементарной работы dA. Величина -

 проекция силы на н аправление п еремещения (рис. 5. 5).
проекция силы на н аправление п еремещения (рис. 5. 5).
Рис. 5. 5
. (5. 4)
Работа переменной силы
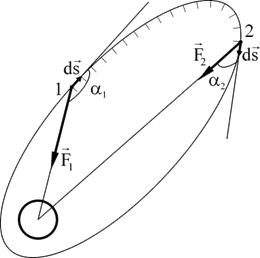
Допустим, мы хотим найти работу, совершаемую гравитационной силой
Земли над еѐ искусственным спутником, который движется по эллиптической
|
|
|
орбите (рис. 5. 6). В этом случае переменными являются и модуль силы F,
и угол, задающий еѐ направление относительно бесконечно малого переме-
щения. Разобьем интересующий нас отрезок траектории от точки 1 до то ч-
ки 2 на бесконечно малые участки длиной ds . Элементарную работу dA на ка ж-
дом таком участке можно найти по фо р-
муле (5. 4). Полная работа равна сумме
бесконечного числа бесконечно малых
элементарных работ dA. Как мы уже зн а-
ем, такая сумма называ ется определенным
интегр алом.
Таким образом, работа переменной
силы находится как определенный инт е-
грал от элемента рной работы (5. 3).
. (5. 5)
Рис. 5. 6 Единица измерения работы – джоуль:
.
Мощность N - это скорость совершения работы, т. е. отношение работы
dA к промежутку времени dt, за который она с овершена:
. (5. 6)
Используя (4. 3) и (2. 1), получим:
, (5. 6а)
здесь v – скорость материальной точки, к которой приложена сила.
Единица мощности
§ 4. Кинетическая энергия
Теперь выясним, как изменяется
состояние движения материальной то ч-
ки при совершении над ней работы. Для
этого мы используем совместно опред е-
ления работы (5. 4), (5. 5) и второй закон
Ньют она.
Применим второй закон Ньютона
(см. (4. 4) и (2. 7)) для материальной то ч-
|
|
|
ки m, движущейся под действием ра в-
Рис. 5. 7 нодейс твующей силы (рис. 5. 7):
. (5. 7)
Помножим (5. 7) скалярно: слева на, справа на
В результате получим:
.
Преобразуем левую часть:
в правой части, в соответствии с (5. 4), запишем dA. В результате этих преобра- зований получим:
. (5. 8) Половина произведения массы частицы материальной точки на квадрат ее
KKKKKKKKKK. о рости названа ее кинетической энергией:
. (5. 9)
Таким образом, элементарная работа, совершаемая над телом, равна эл е-
ментарному приращению его кинетической энергии. При интегрировании фо р-
мулы (5. 8) вдоль траектории частицы, от точки 1 до точки 2 (рис. 5. 7), мы пол у-
чим:
,
где слева стоит интеграл от дифференциала, справа – (см. (5. 5)). После и н-
тегрирования имеем:
. (5. 10) Используя обозначение (5. 9) для кинетической энергии, формулу (5. 10)
можно записать так:
. (5. 11) Применив второй закон Ньютона и определение работы, мы получили, что
работа равнодействующей силы идет на приращение кинетической энергии
матер иальной точки (5. 10).
Это утверждение носит название теоремы о кинетической энергии.
ИТОГИ ЛЕКЦИИ № 5
1. Импульс системы материальных точек – это векторная сумма импульсов
всех материальных точек, входящих в систему (5. 1):
2. Система называется замкнутой, если на нее не действуют внешние силы.
3. Импульс системы сохраняется, т. е. не изменяется с течением времени,
если векторная сумма всех внешних сил, действующих на систему, равна н улю.
В частности, сохраняется импульс замкнутой системы.
|
|
|
4. Работа постоянной силы равна скалярному произведению векторов силы
и пере мещения (5. 3):
5. Работа переменной силы (5. 5) находится как определенный интеграл от
элементарной работы (5. 4):
.
6. Мощность – это скорость совершения работы (5. 5):
.
7. Кинетической энергией (5. 9) называют половину произведения
массы частицы m на квадрат ее скорости:
8. Теорема о кинетической энергии ((5. 10) и (5. 11)) утверждает, что работа
равнодействующей силы идет на приращение кинет ической энергии (5. 9):
ЛЕКЦИЯ № 6
|
|
|


