 |
4.2. Общие формулы для дифференциального дроссель-эффекта
|
|
|
|
4. 2. Общие формулы для дифференциального дроссель-эффекта
Как известно из общей термодинамики, энтальпия является функцией состояния, поэтому di является полным дифференциалом.
На этом основании, полагая i = i(T, P), получим по правилам математики
.
Значения частных производных в этом уравнении определяются из первого начала термодинамики, записанного в энтальпийной форме:
.
− Так как 
, то при P = const, 
, dP = 0 и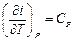 
.
− Так как 
, то 
, откуда при Т = const
.
Эта частная производная относится ко второму типу дифференциальных соотношений термодинамики, поэтому
.
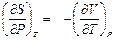Тогда
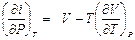
и
.
Интегрирование этого уравнения приводит к следующему результату:
.
Так как при дросселировании i2 = i1, то
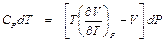
или
.
Интегрирование этого уравнения дает
.
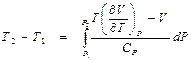Из сравнения этого результата с формулой (4. 3) для интегрального дроссель-эффекта следует:
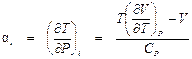. (4. 4)
В этой формуле T, V, CP относятся к состоянию рабочего тела перед дросселем.
Ранее было показано, что при дросселировании идеального газа его температура не изменяется. Этот же результат можно получить, если в формулу для дифференциального дроссель-эффекта подставить значение частной производной для идеального газа.
Как известно из общей термодинамики для идеального газа
.
Тогда
.
Таким образом, у идеального газа α i = 0 при всех значениях давления и температуры.
У реальных газов значения Ср, V, 
зависят от величины давления и температуры, поэтому α i у этих газов так же зависит от Р и Т.
Можно получить еще одну формулу для α i, если выразить частную производную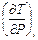 
как произведение двух частных производных:
|
|
|
.
Задача при этом сводится к нахождению значений этих двух частных производных и выражения их через частные производные, не содержащие энтальпию i.
Подробный вывод второй формулы для α i в варианте автора данного пособия дается в приложении (П. 1).
. (4. 5)
Эта формула очень удобна для исследования процесса дросселирования в различных областях фазовых состояний вещества.
5. Дифференциальный дроссель-эффект в области двухфазных состояний вещества
В данном случае под двухфазным состоянием вещества понимается область его влажного насыщенного пара (ВНП).
Рис. 5. 1. Фазовая P-V диаграмма вещества
На рис. 5. 1 это область внутри пограничной кривой – совокупности нижней (х = 0) и верхней (х = 1) пограничных кривых.
Как известно, в области двухфазных состояний вещества изотермические процессы (Т = const) являются одновременно и изобарными (отрезок С'С'').
Таким образом, в двухфазной области (ВНП)
.
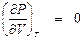При этом формула (4. 5) для α i принимает вид:
.
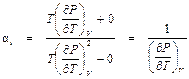Но в области двухфазных состояний значение РН зависит только от ТН и не зависит от величины удельного объема (см. рис. 5. 1), поэтому в области ВНП
.
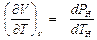Окончательно
. (5. 1)
Как следует из фазовой Р-Т диаграммы (рис 5. 2), угловой коэффициент кривой АК (геометрическое место точек равновесного сосуществования жидкости «Ж» и пара «П»), всегда положителен
,
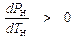и поэтому
. (5. 2)
Рис. 5. 2. Фазовая Р-Т диаграмма
Таким образом, дросселирование в области ВНП всегда приводит к понижению температуры. Это хорошо иллюстрируется i-S диаграммой (рис. 5. 3).
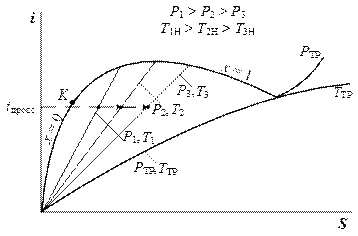
Рис. 5. 3. Процесс дросселирования на i-S диаграмме.
|
|
|
Как известно, РН и ТН связаны уравнением Клайперона-Клаузиуса:
.
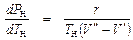Все точки на кривой АК (рис. 5. 2) подчиняются этому уравнению. Поэтому
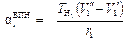. (5. 3)
Здесь V1' и V1'' – удельный объем (м3/кг) сухого насыщенного пара вещества и его кипящей (насыщенной) жидкости при начальном давлении дросселирования Р1 (Па);
и r1 – абсолютная температура насыщения (°К) и скрытая теплота парообразования (Дж/кг) при давлении Р1.
С ростом давления отношение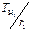 
растет, но разность 
убывает быстрее, поэтому с ростом Р1 величина 
убывает.
|
|
|
