8. Инверсионная кривая

 

Геометрическое место точек инверсии называется инверсионной кривой. Инверсионная кривая – это совокупность левой и правой инверсионных кривых. На левой инверсионной кривой лежат все нижние точки инверсии, а на правой – все верхние.

Построение инверсионной кривой в P-V координатах иллюстрируется рис. 8. 1.

Как следует из рис. 8. 1. инверсионная кривая огибает пограничную кривую. Внутри инверсионной кривой α _i > 0, т. е. дросселирование вызывает уменьшение температуры, а вне (α _i < 0) – увеличение температуры рабочего тела.

 

Рис. 8. 1. Построение инверсионной кривой в Р-V координатах

 

Из рис. 8. 1. так же следует, что при давлении ниже критического Р_К нижние точки инверсии соответствуют дросселированию жидкости, так как находятся левее нижней пограничной кривой вещества (х = 0). Верхние точки инверсии располагаются правее верхней пограничной кривой (х = 1) и поэтому соответствуют дросселированию газа.

Как известно, пар – это газообразное состояние вещества при температуре ниже критической. Критическая изотерма, как видно из рис. 8. 1, располагается внутри инверсионной кривой, поэтому вся область перегретого пара находится внутри инверсионной кривой, где α _i > 0. Таким образом, при адиабатном дросселировании перегретый пар охлаждается.

Инверсионную кривую обычно представляют в Р-Т координатах (рис. 8. 2). При начальном давлении дросселирования 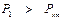 с любой начальной температурой t₁, всегда α _i < 0, т. е. дросселирование сопровождается нагреванием газа. При любом начальном давлении Р₁ с начальной температурой дросселирования  дросселирование также всегда приводит к нагреванию газа (α _i < 0).

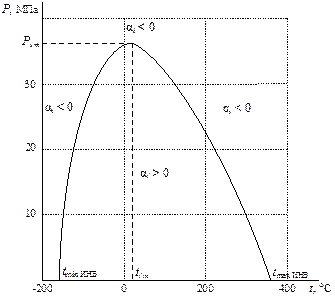
Рис. 8. 2. Инверсионная кривая для азота

 

Для того, чтобы получить эффект охлаждения, необходимо так понизить начальную температуру t₁, чтобы точка с координатами (Р₁, t₁) оказались внутри инверсионной кривой.

При  дросселирование также приводит к нагреванию рабочего тела при любых значениях начального давления Р₁. В этом случае, для того, чтобы получить эффект охлаждения, необходимо так повысить начальную температуру t₁, чтобы точка с координатами (Р₁, t₁) оказалась внутри инверсионной кривой. Таким образом, дросселирование приводит к охлаждению рабочего тела (жидкости или пара) при всех сочетаниях термодинамических параметров состояния вещества перед дросселем (Р₁, t₁), соответствующих точкам внутри области, ограниченной сверху инверсионной кривой.

Для получения уравнения инверсионной кривой в явном виде необходимо знать уравнение состояния данного вещества и использовать его в формулах (4. 4) или (4. 5) при α _i = 0:

                                      (8. 1)

или

 

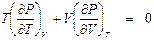.                               (8. 2)

 

Уравнения (8. 1) и (8. 2) называются уравнениями инверсионной кривой.

Если продифференцировать (8. 1), полагая Р и V функциями температуры, то можно получить еще одно уравнение инверсионной кривой в общем виде:

 

.              (8. 3)

 

Подробный вывод этого уравнения в варианте автора данного пособия дается в приложении (П. 2).

В точке максимума на инверсионной кривой (рис. 8. 2) 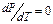, поэтому для выполнения равенства (8. 3) необходимо, чтобы

 

.

 

Так как Т ≠ 0, то окончательно условие максимума инверсионной кривой приобретает следующий вид:

 

.                                             (8. 4)

 

Для того, чтобы записать это уравнение в явном виде, необходимо знать конкретный вид уравнения состояния реального газа (Ван-дер-Ваальса, Дюпре и др. ).

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: