 |
6. Дифференциальный дроссель-эффект в критической точке
|
|
|
|
6. Дифференциальный дроссель-эффект в критической точке
В критической точке (точка К) как следует из рис. 5. 1 
, а из рис. 5. 2 – 
.
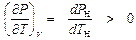Поэтому из формулы (4. 5)
. (6. 1)
Таким образом, в критической точке для всех веществ дифференциальный дроссель-эффект (α i) равен обратной величине углового коэффициента кривой АК в точке К на Р-Т диаграмме.
Как известно, в критической точке rК = 0 и 
, поэтому
.
Эта неопределенность может быть раскрыта, но для этого должны быть известны зависимости r = r (T), 
и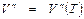 
.
Для нахождения 
лучше всего воспользоваться формулой
,
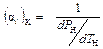в которой производная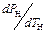 
в точке К определяется из уравнения состояния реального газа (Ван-дер-Ваальса, Дюпре, Вукаловича-Новикова и др. )
7. Дифференциальный дроссель-эффект в однофазных областях. Точки инверсии
Для анализа изменения α i в этих областях лучше всего воспользоваться первым уравнением (4. 4):
. (4. 4)
Частная производная 
определяется по формуле П1. 11 (приложение П1):
,
откуда
. (7. 1)
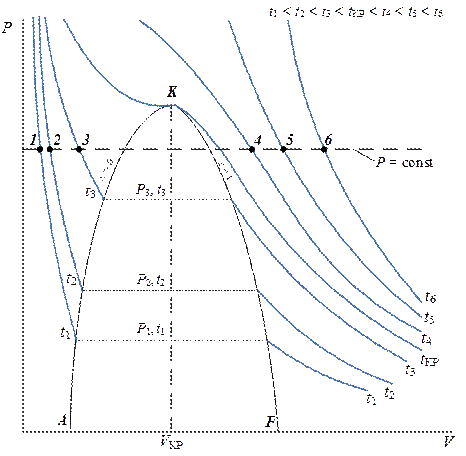
Рис. 7. 1. Изотермы в P-V диаграмме реального газа
Для газов повышение температуры при постоянном объеме всегда вызывает рост давления, т. е.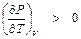 
.
Таким образом, для определения характера изменения в формуле (7. 1) величины 
при изменении температуры в условиях P = const, необходимо знать характер изменения величины изотермической упругости 
, которая всегда меньше нуля.
Как известно, частная производная 
– это угловой коэффициент кривой 
при заданной температуре Т (в Р-V координатах это тангенс угла наклона к оси V касательной в данной точке к кривой P = P(V)).
|
|
|
Как следует из рис. 7. 1. при P = const вне пограничной кривой AKF слева и справа от изохоры VКР = const, повышение температуры вызывает разное по знаку изменение 
.
Справа от прямой VКР = const в точках пересечения с изотермами t4 = const, t5 = const и t6 = const (точки 4, 5 и 6 соответственно) угол наклона касательных к оси V возрастает по мере увеличения температуры.
Слева от прямой VКР = const в точках пересечения изобары P = const с изотермами t1 = const, t2 = const и t3 = const (точки 1, 2 и 3 соответственно) угловой коэффициент изотермы в этих точках (крутизна изотерм) наоборот убывает с повышением температуры.
Таким образом, для любого значения P = const, не превышающего некоторое значение Pim > PK (см. следующий параграф) должны существовать две изотермы (обозначенные 
и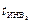 
), у которых в точках пересечения с изобарой P = const выполняется равенство:
.
Изотерма 
расположена слева от изохоры VКР = const, а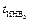 
– справа.
Числитель формулы (4. 4) при этом становится равным нулю и дифференциальный дроссель-эффект α i в этих точках, нижней и верхней, также обращается в нуль.
Дальнейший переход от «верхней» точки к изотермам с более высокими температурами ( 
) приведет к тому, что будет выполняться неравенство
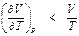, то есть α i поменяет знак на отрицательный.
Переход от «нижней» точки к изотермам с меньшими температурами ( 
) также приведет к выполнению неравенства 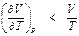, т. е. α i также поменяет знак с положительного на отрицательный.
Состояние, при котором α i меняет знак, называется точкой инверсии.
Таким образом, точки, которые выше обозначались как «нижняя» и «верхняя», являются нижней и верхней инверсионными точками при заданном значении Р. При другом значении Р существуют две другие точки инверсии и т. д.
Таким образом, множеству значений Р < Pim соответствует такое же множество пар точек инверсии.
|
|
|
|
|
|
