 |
Значения постоянных Ван-дер-Ваальса для водяного пара при R = Rμ/μ
|
|
|
|
Значения постоянных Ван-дер-Ваальса для водяного пара при R = Rμ /μ
| Номер варианта сочетания определяющих параметров | Определяющие параметры | а, Н∙ м4/кг2 | b, м3/кг |
| РК и ТК | 0, 001687 | ||
| VК и ТК | 0, 001087 | ||
| РК и VК | 0, 001087 |
При расчете R по формуле (9. 8) при известных TК, VК и РК получено: а = 706 Н∙ м4/кг2, b = 0, 001087 м3/кг.
Предпочтительным является вариант 1 сочетания определяющих параметров, т. к. в специальных опытах по определению термодинамических параметров в критической точке, значения РК и TК определяются значительно точнее, чем VК.
Недостатком метода вычисления постоянных a и b при R, взятом по идеальному газу, является то, что критическая изотерма, рассчитанная по уравнению Ван-дер-Ваальса при всех трех вариантах сочетания определяющих параметров, не проходит через критическую точку. Ближе всего к ней проходит изотерма, рассчитанная при a и b, найденных по варианту 1.
От этого недостатка свободен метод определения a, b и R по формулам (9. 8), но при этом уравнение Ван-дер-Ваальса, записанное в форме
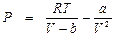, (9. 9)
при Р → 0 не обращается в равенство, как у идеального газа, поскольку правая часть уравнения (9. 9) не стремится к нулю. Кроме того, в этом методе коэффициент сжимаемости в критической точке ( 
) получается для всех веществ одинаковым и равным 3/8 = 0, 375, т. е. заметно отличается от разнообразных значений ZК в табл. 9. 1, полученных для различных веществ.
Таким образом, определение постоянных уравнения Ван-дер-Ваальса через параметры TК, VК, РК приводит к серьезным трудностям. Главная причина этих трудностей в том, что уравнение Ван-дер-Ваальса, строго говоря, удовлетворительно применимо лишь в области невысоких давлений, поэтому в области критической точки оно не отличается достаточной точностью, и описывает свойства реальных газов при высоких давлениях лишь приблизительно.
|
|
|
Однако, это уравнение вполне применимо для качественных оценок при анализе некоторых закономерностей поведения реальных газов, в частности при дросселировании.
9. 2. Качественный анализ процесса дросселирования с помощью уравнения Ван-дер-Ваальса
9. 2. 1. Построение инверсионной кривой
Как указывалось в п. 8, для получения инверсионной кривой необходимо знать конкретный вид уравнения состояния реального газа. Предположим, что реальный газ подчиняется уравнению Ван-дер-Ваальса.
Для вычисления дифференциального дроссель-эффекта по зависимости (4. 4) необходимо знать частную производную 
для реального газа.
Запишем уравнение Ван-дер-Ваальса в виде:
. (9. 10)
После дифференцирования этого уравнения при P = const получим:
,
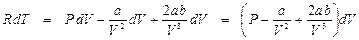откуда
. (9. 11)
После подстановки уравнения (9. 11) в уравнение (4. 4) получим:
. (9. 12)
Значения постоянных Ван-дер-Ваальса возьмем при определяющих параметрах TК и РК:
; 
; 
.
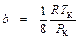Как было указано в параграфе 9. 1, при таком варианте сочетаний определяющих параметров, расчетная критическая изотерма ближе всего подходит к критической точке.
Для построения кривых зависимости дифференциального дроссель-эффекта от температуры при P = const, задаемся рядом значений V, затем по формуле (9. 10) определяем Т, после чего эти V и Т подставляем в уравнение (9. 12).
На рис. 9. 2 представлены графически результаты определения α i для воздуха [1].
В расчетах принималось: TК = 133, 46 °К, РК = 3, 7 МПа, СР = 1015 Дж/(кг°К), R = 287 Дж/(кг°К). При этих исходных данных по формулам (9. 8) определены значения двух остальных постоянных уравнения Ван-дер-Ваальса:
|
|
|
а = 164, 78 (Н∙ м4)/кг2; b = 1, 28∙ 10-3 м3/кг.
На рис. 9. 2 точки пересечения кривых 
с осью температуры при P = const являются точками инверсии для данного давления Р. Из двух точек пересечения меньшему значению температуры соответствует нижняя точка инверсии, а большему значению Т – верхняя.
Рис. 9. 2. Дифференциальный дроссель-эффект в зависимости от температуры перед дросселированием при различных начальных давлениях воздуха.
Точки инверсии, перенесенные в Р-Т координаты и соединенные плавной кривой, дают инверсионную кривую (рис. 9. 3). Относительное превышение давления в точке максимума инверсионной кривой (Рim) над критическим давлением воздуха (РК = 3, 7 МПа) по расчетам составляет Рi m/ РК = 9 (в опытах для воздуха Рi m/ РК = 10, 8).
Рис. 9. 3. Инверсионная кривая воздуха [1]
Аналогичным образом на рис. 9. 4 построена расчетная инверсионная кривая для кислорода (ТК = 154, 58 °К, РК = 5, 043 МПа), из которой следует, что давление в точке максимума кривой инверсии (Рim) в девять раз превышает критическое давление РК (в опытах для кислорода Рi m/РК = 12).
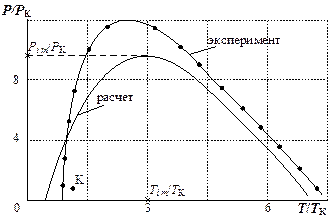
Рис. 9. 4. Инверсионная кривая кислорода в относительных параметрах [2]
При Р = 0, 1 МПа большинство газов имеют довольно высокую температуру верхней точки инверсии (800 °К и более), за исключением водорода (193 °К) и гелия (37 °К).
|
|
|
