 |
9.3. Расчетное определение термодинамических параметров в точке максимума инверсионной кривой
|
|
|
|
9. 3. Расчетное определение термодинамических параметров в точке максимума инверсионной кривой
Определим параметры точки максимума инверсионной кривой (Vi m, Ti m, Рi m) через параметры критической точки (VК, TК, РК). В соответствии с (8. 4), условием максимума инверсионной кривой в общем случае является равенство:
.
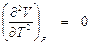По формуле (9. 11)
.
Подставим в это уравнение значение Р, выраженное в явном виде (9. 9) из уравнения Ван-дер-Ваальса:
.
Тогда
или
. (9. 13)
Эта формула для анализа удобнее (9. 11), поскольку не содержит Р. Продифференцировав (9. 13) по Т при Р = const, получим:
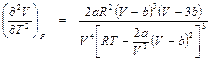. (9. 14)
Эта формула обращается в нуль, если V = 3b (как показывалось выше, V > > b).
Но в соответствии с уравнением (9. 7) равенство V = 3b выполняется только в критической точке. Так как (9. 14) обращается в нуль при V = VК, то в точке максимума кривой инверсии объем газа равен VК:
Vi m = VК = 3b. (9. 15)
Таким образом, в P-V координатах точки Рi m и РК находятся на одной прямой VК = const.
В точке максимума инверсионной кривой выполняется условие 
, которое в соответствии с (9. 5) принимает вид:
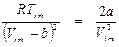
или
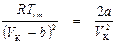
или
,
откуда
.
Но из (9. 7)
,
следовательно
. (9. 16)
Таким образом, в соответствии с уравнением Ван-дер-Ваальса, в точке максимума инверсионной кривой температура должна в три раза превышать критическую.
Уравнение (9. 9) для точки максимума инверсионной кривой имеет вид:
.
Так как Vi m = VК = 3b, а Ti m = 3TК, то
,
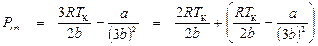где 
.
|
|
|
Тогда
.
Но из (9. 8):
.
Окончательно
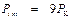. (9. 17)
Таким образом, в соответствии с уравнением Ван-дер-Ваальса, в точке максимума инверсионной кривой давление должно в 9 раз превышать критическое.
Средние значения термодинамических параметров в точке максимума инверсионной кривой, полученные в экспериментах, составляют:
, 
, 
.
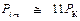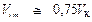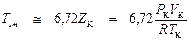Это среднее значение Ti m для различных веществ составляет (1, 62 ÷ 2, 06)ТК.
Как следует из рис. 9. 3 и рис. 9. 4 результаты расчетного определения Vim, Tim и Рim количественно удовлетворительно согласуются с их значениями, полученными в экспериментах.
Качественно инверсионные кривые, полученные с использованием уравнения Ван-дер-Ваальса, правильно описывают реальные процессы, что очень важно для выяснения сути процессов дросселирования и анализа их результатов.
9. 4. Расчетное определение максимальной и минимальной температуры инверсии
Определим максимальное значение температуры верхних точек инверсии (ТИНВ max) и минимальной температуры нижних точек инверсии (ТИНВ min), нанесенных на рис. 8. 2.
Для правой ветви инверсионной кривой можно получить приближенное выражение для α i:
. (9. 18)
Вариант вывода этой формулы, предложенный автором, дается в Приложении (П. 3).
Это уравнение применимо для малых плотностей газов, которые бывают при малых давлениях (Р → 0) и высоких температурах. Поэтому, для получения ТИНВ max, приравняем α i в уравнении (9. 18) к нулю при Р = 0:
,
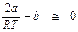откуда
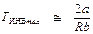. (9. 19)
После подстановки в эту формулу значений a и b из (9. 8) получим:
.
Окончательно
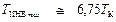. (9. 20)
Таким образом, правая ветвь инверсионной кривой пересекает ость Т в точке с очень высокой температурой 6, 75ТК.
|
|
|
Экспериментальное определение ТИНВ max затруднено из-за высоких температур. Ориентировочно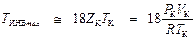 
.
Если взять R по идеальному газу R = Rμ /μ, то ZК = 0, 375 и то 
.
Для различных реальных газов, представленных в табл. 9. 1, ZК = 0, 23 ÷ 0, 33, поэтому 
.
Левая ветвь инверсионной кривой доходит до кривой до насыщения жидкости АК (рис. 9. 5, но не должна пересекать ее. Как было показано в параграфе 5, для всех точек двухфазного состояния вещества на кривой АК α i > 0, поэтому точки пересечения кривой инверсии (α i = 0) с кривой АК (α i > 0) быть не может.
Рис. 9. 5. Инверсионная кривая на фазовой Р-Т диаграмме нормального вещества
В работе [2] приводится значение ТИНВ min = 0, 75 ТК. Эта величина формально получается из уравнения (9. 10) при Р = 0 и V = VК:
.
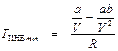Подставляя в это уравнение значения a, b и VКР из уравнения (9. 8), получим:
.
Окончательно
. (9. 21)
Можно показать (рис. 9. 6), что изохоры с V < VКР расположены на Р-Т диаграмме в однофазной области «Ж» выше и левее кривой насыщения АК, а изохоры с V > VКР – в другой однофазной области (перегретый пар или газ) ниже и правее кривой насыщения.
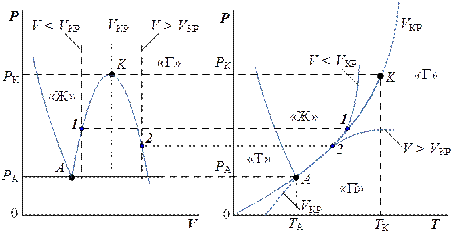
Рис. 9. 6. Расположение изохор V ≠ VКР относительно кривой насыщения
(Точка 1 соответствует пересечению изохоры V < VКР с нижней пограничной кривой (х = 0) на P-V диаграмме, а точка 2 – изохоры V > VКР с верхней пограничной кривой (х = 1)).
Так как в процессах нагревания или охлаждения при V = VКР и Р < РКР двухфазное состояние вещества сохраняется от тройной точки А до критической точки К, то изохора VКР на Р-Т диаграмме совпадает с кривой насыщения АК.
При Р > РКР изохора VКР является плавным продолжением кривой насыщения АК.
В точке А кривая насыщения и критическая изохора (VКР = const) также имеют общую касательную, поэтому в области Р < РА изохора VКР является плавным продолжением кривой насыщения.
Таким образом, точка ТИНВ min, найденная по уравнению (9. 21), является точкой пересечения продолжения кривой насыщения АК с осью Т.
Можно предположить, что левая ветвь инверсионной кривой насыщения АК, далее «скользит» по ней, не касаясь, до тройной точки А. При этом пересечения с осью Т не будет, и левая ветвь инверсионной кривой оборвется в точке с координатами ТА и Р ≈ РА, т. е. вблизи тройной точки.
|
|
|
При решении практических задач можно полагать, что кривая инверсии обрывается в точке встречи с кривой насыщения с примерными координатами Т = 0, 75ТКР и Р ≈ 0.
|
|
|
