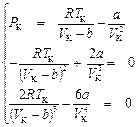 |
9. Дросселирование рабочего тела, подчиняющегося уравнению Ван-дер-Ваальса
|
|
|
|
9. Дросселирование рабочего тела, подчиняющегося уравнению Ван-дер-Ваальса
Как указывалось выше, для определения дифференциального дроссель-эффекта и инверсионной кривой необходимо знание уравнения состояния реального газа. В качестве примера обычно рассматривается уравнение состояния реального газа, предложенное Ван-дер-Ваальсом.
9. 1. Основные сведения об уравнении Ван-дер-Ваальса
Нидерландский физик Ян Дидерик Ван-дер-Ваальс (1837 – 1923) – лауреат Нобелевской премии 1910 г., вывел в 1873 г. уравнение состояния неидеального газа в виде:
, (9. 1)
учитывающем конечность объема молекул и наличие сил межмолекулярного притяжения.
Здесь a, b, R – постоянные, индивидуальные для каждого вещества;
– поправка, учитывающая уменьшение давления из-за взаимного притяжения молекул; силы взаимного притяжения молекул создают в тонком слое у стенки сосуда равнодействующую силу, направленную внутрь объема;
b – поправка, учитывающая собственный объем молекул и силы отталкивания между ними.
Для определения индивидуальных постоянных, необходимы экспериментальные измерения Р, Т, V хотя бы для трех состояний.
Часто численные значения постоянных a, b и R определяются по критическим параметрам вещества (РК, ТК, VК), найденным экспериментально.
В таблице 9. 1. представлены значения критических параметров и коэффициента сжимаемости в критической точке ZК для некоторых веществ, где 
, и величина R взята по идеальному газу, т. е. 
.
Таблица 9. 1.
Критические параметры и ZК для некоторых веществ
| Вещество | Химическая формула | ТК, °К | РК, МПа | VК∙ 103, м3/кг | ZК |
| Азот | N2 | 126, 20 | 3, 400 | 3, 194 | 0, 290 |
| Аммиак | NH3 | 405, 50 | 10, 93 | 4, 255 | 0, 238 |
| Вода | H2O | 647, 27 | 22, 115 | 3, 147 | 0, 239 |
| Водород | H2 | 33, 25 | 1, 320 | 32, 50 | 0, 320 |
| Кислород | O2 | 154, 58 | 5, 043 | 2, 30 | 0, 290 |
| Метан | CH4 | 190, 77 | 4, 626 | 6, 116 | 0, 284 |
| Окись углерода | CO | 132, 90 | 3, 500 | 3, 325 | 0, 295 |
| Углекислый газ | CO2 | 304, 20 | 7, 383 | 2, 136 | 0, 274 |
|
|
|
На рис. 9. 1. приведены изотермы Ван-дер-Ваальса. В области двухфазного состояния вещества (влажного насыщенного пара) они имеют волнообразный характер, что отличает их от реальных изотерм, представляющих прямые, параллельные оси V (например, С'С''). Эти волнообразные участки объясняются тем, что уравнение Ван-дер-Ваальса является уравнением третьей степени относительно V и, поэтому, может иметь либо три, либо один вещественный корень при различных Р и Т. Один вещественный корень существует только при 
.
Рис. 9. 1. Изотермы Ван-дер-Ваальса
В критической точке изотерма tКР имеет точку перегиба, поэтому в этой точке выполняются два условия:
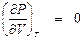(9. 2)
и
(9. 3)
Таким образом, для определения трех неизвестных постоянных (a, b и R) есть три уравнения, полученные из уравнений (9. 1 – 9. 3):
|
| (9. 4) |
| (9. 5) | |
| (9. 6) |
Температуру TК и удельный объем VК можно определить из уравнений (9. 5), (9. 6) и затем определить РК из уравнения (9. 4).
В итоге
; 
; 
. (9. 7)
Отсюда
; 
; 
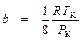. (9. 8)
Найденное по формуле (9. 8) значение R отличается от общепринятых значений, взятых по идеальному газу:
.
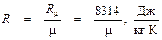Так, для водяного пара при значениях TК, VК и РК, взятых из таблицы 9. 1, величина R по формуле (9. 8) равна 297, 2 
, в то время, как по идеальному газу
.
Общим требованием ко всем уравнениям состояния реального газа является обращение их в уравнение Менделеева-Клайперона (PV = RT) при V → ∞. Уравнение Ван-дер-Ваальса при V > > b переходит в уравнение состояния идеального газа, если значение R взято по идеальному газу. Если брать R по идеальному газу, т. е. не определять ее по третьему уравнению (9. 8), то для нахождения двух оставшихся постоянных (a и b) имеется три исходных уравнения (9. 4), (9. 5) и (9. 6). Эта ситуация означает неопределенность в вычислении постоянных a и b, так как их значения зависят в этом случае от того, какая пара термодинамических параметров взята в качестве определяющих: РК и ТК, VК и ТК, РК и VК. В зависимости от выбора определяющей пары термодинамических параметров получаются различные значения постоянных a и b. В качестве примера в таблице 9. 2 представлены результаты расчета постоянных Ван-дер-Ваальса для водяного пара при различных вариантах сочетания двух определяющих параметров.
|
|
|
Таблица 9. 2.
|
|
|
