10. Сравнение дроссель-эффекта с температурным эффектом адиабатного расширения

10. Сравнение дроссель-эффекта с температурным эффектом адиабатного расширения

 

Из курса общей термодинамики (раздел «Вычисление энтропии») известно соотношение:

 

.

 

Для обратимого адиабатного процесса (dS = 0) это уравнение приобретает следующий вид:

 

,

 

откуда следует

 

.

 

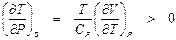    Обозначим температурный эффект обратимого адиабатного расширения как .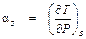

 

.                                     (10. 1)

        

    Сравним α _S с дроссель-эффектом α _i (примечание: α _i иногда называют температурным эффектом необратимого адиабатного процесса расширения).

 

.

 

Окончательно

 

.                     (10. 2)

 

Из уравнения (10. 2) следует, что при адиабатном расширении газ охлаждается сильнее, чем при адиабатном дросселировании.

Для получения низких температур, например, сжижение газов, целесообразно использовать детандеры – расширительные цилиндры, в которых производится адиабатное расширение газа.

Как было показано выше, охлаждение рабочего тела при дросселировании   (α _i > 0), возможно лишь при расположении начальных точек дросселирования (Р₁, Т₁) в определенных областях,

Так, например, при Т₁> Т_{ИНВ max} охлаждение газа при дросселировании невозможно ни при каких значениях начального давления Р₁.

В случае адиабатного расширения охлаждение рабочего тела (даже идеального газа) достигается всегда, при любом сочетании начальных значений термодинамических параметров (Р₁, Т₁).

Последнее является большим достоинством метода охлаждения за счет адиабатного расширения. Недостатком этого метода является техническая сложность осуществления регулирования температуры охлаждения. Метод дросселирования свободен от этого недостатка, но приводит к некоторому снижению эффективности работы холодильной установки.

Как следует из уравнения (10. 2), в области двухфазных состояний вещества, где С_Р → ∞, α _S = α _i, т. е. одинаковый перепад давления Р₁ – Р₂, приводит к одинаковому понижению температуры Т₁ – Т₂. Чем больше реальный процесс адиабатного расширения газа в детандере отличается от обратимого действием сил трения, ведущих к нагреванию газа, тем сильнее α _S стремится к α _i.

Процесс дросселирования из-за его необратимости приводит к снижению работоспособности газа (пара) по сравнению с адиабатным обратимым расширением. Рассмотрим два варианта расширения пара от P₁ до P₃:

1. адиабатное обратимое расширение, при котором теоретическая работа пара равна разности i₁ – i₃;
2. дросселирование пара от Р₁ до Р₂ (Р₂ > Р₃) с последующим адиабатным расширением пара от Р₂ до Р₃.

Теоретическая работа пара при таком варианте расширения будет меньше и равна разности i₂ – i₄, где i₂ = i₁, а i₄ > i₃. Это иллюстрируется рис. 10. 1

 

Рис. 10. 1. Влияние процесса дросселирования на работоспособность пара

 

Потеря работоспособности 1 кг пара в приведенном примере составит:

 

.

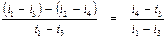Приложение

 

П. 1. Вывод формулы для дифференциального дроссель-эффекта (вариант автора пособия)

 

.                          (П1. 1)

 

а) Определим для формулы (П1. 1). Пусть i = i(T, V),

тогда

 

,

 

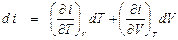откуда

.                               (П1. 2)

 

б) Определим . Пусть i = i(Р, V),

тогда

 

,

 

откуда

 

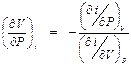.                            (П1. 3)

 

в) После подстановки (П1. 2) и (П1. 3) в уравнение (П1. 1) имеем:

 

,

 

.                                           (П1. 4)

 

г) Определим . Так как i = U + PV, то di =dU + PdV + VdP,

откуда:

 

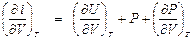.                         (П1. 5)

 

Определим . Так как dU = ТdS – PdV,

то:

 

.

        

По третьему типу дифференциальных соотношений термодинамики

 

.

 

Тогда

 

.                              (П1. 6)

 

Подставим (П1. 6) в уравнение (П1. 5):

 

,

 

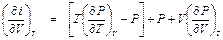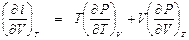.                          (П1. 7)

 

д) Определим для формулы (П1. 4). Представим эту производную в виде произведения двух частных производных:

 

.

 

Из общей термодинамики известно, что = С_Р.

Тогда

 

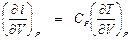.                               (П1. 8)

 

Общая формула для теплоемкостей однородных систем, как известно из общей термодинамик, имеет вид:

 

.

 

Для изобарного процесса из этой формулы следует:

 

 

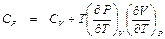.                        (П1. 9)

 

Подставим (П1. 9) в (П1. 8):

 

 

и

.                        (П1. 10)

 

е) Подставим П(1. 10) и (П1. 7) в формулу (П1. 4):

 

.

 

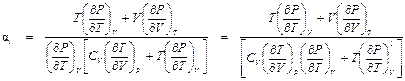Выразим произведение 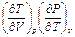 в знаменателе через произведение других частных производных, используя дифференциальные соотношения термодинамики:

 

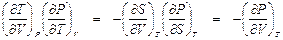.          (П1. 11)

 

Тогда окончательно

.                             (П1. 12)

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: