 |
5.3. Решение уравнения Шредингера в области E<0
|
|
|
|
5. 3. Решение уравнения Шредингера в области E< 0
Решением уравнения Шредингера (5), в области E< 0, для основного состояния электрона (n = 1), является:
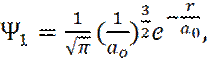(6)
где a0 – радиус первой орбиты Бора.
Соответственно, решение для энергии электрона получается квантованным:
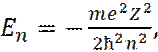(7)
где n=1, 2, 3, … - главное квантовое число; me - масса электрона; Z – заряд ядра.
Если энергию электрона выразить в электрон-вольтах, то выражение (8) запишется:
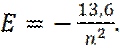(9)
5. 4. Квантование волновой функции Ψ (r, θ, φ )
Поскольку решение уравнения Шредингера ищется в сферических пространственных координатах, то получаемая волновая функция квантуется по координатам r, θ, φ и зависит от 3-х квантовых чисел:
n –главного квантового числа; l – орбитального квантового числа; m – магнитного квантового числа.
Отметим, что общая энергия электрона En, в силу симметрии зависит лишь от n.
Квантование волновой функциивозникает в силу требований к ней конечности и непрерывности.
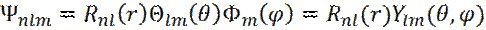(10)
Волновая функция (10) называется атомной орбиталью.
Орбитальное квантовое число l – определяет характер симметрии (форму) электронного облака. Так, при l = 0 наблюдается сферическая симметрия.
Значения l часто обозначаются буквами:
Значения квантового числа l меняются от 0 до n-1.
Магнитное квантовое число m характеризует расположение атомной орбитали в пространстве. Значения магнитного квантового числа m меняются от - l до + l.
В 1925 году было обнаружено, что электрон имеет собственный момент (спин). Соответственно происходит расщепление энергетических уровней в зависимости от значения спинового квантового числа ms = ± ½.
Таким образом, основное состояние электрона в атоме водорода характеризуется 4-мя квантовыми числами: n = 1, l = 0, m = 0, ms = ± ½.
|
|
|
Энергия электрона зависит только от главного квантового числа n.
Соответственно, состояния электрона при различных l, m, ms, называются вырожденными, а число таких состояний – кратностью вырождения уровня n.
5. 5. Влияние орбитального квантового числа ℓ на форму электронного облака
s-, p- и d - орбитали атомов соответствуют орбитальным квантовым числам ℓ = 0, 1, 2. Числа справа: 1, 2 и 3 — значения главного квантового числа n.
5. 6. Кратность вырождения различных энергетических уровней
Оценим кратность вырождения N для различных значений главного квантового числа n:
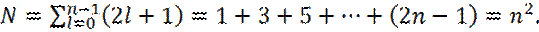(11)
Отметим, что под суммой в уравнении (11) стоит арифметическая прогрессия, сумма членов s которой равна:
.
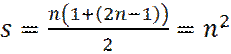С учетом 2-х значений спинового квантового числа ms = ± ½ имеем кратность вырождения n –го энергетического уровня, равную 2n2.
5. 7. Средний радиус орбитали электрона в атоме водорода
Значения волновой функции позволяют вычислить любые свойства атомно-молекулярной системы. В качестве примера определим средний радиус орбитали электрона в атоме водорода в основном состоянии ( n=1, l=0, m=0 ).
Волновая функция для основного состояния электрона имеет вид:
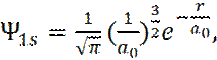(12)
где a0 –радиус первой орбиты Бора:
ε 0 – диэлектрическая постоянная вакуума.
Учитывая, что |Ψ 1s |2 является функцией плотности распределения электрона, имеем следующее:
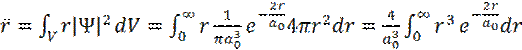(13)
Интеграл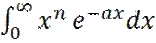 
является табличным и равен:
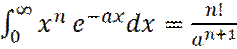(14)
Тогда, т. к. у нас n=3 получаем следующее выражение для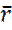 
:
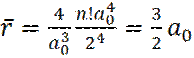(15)
Таким образом, средний радиус орбитали электрона в основном состоянии в атоме водорода в полтора раза больше боровской орбиты a0.
5. 8. Наиболее вероятный радиус орбиты электрона в атоме водорода в основном состоянии
Определим наиболее вероятное расстояние электрона от ядра атома водорода в основном состоянии ( n=1, l=0, m=0 ).
|
|
|
Используя определение функции плотности вероятности f распределения электрона через волновую функцию Ψ :
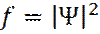(16)
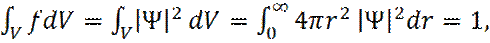(17)
имеем:
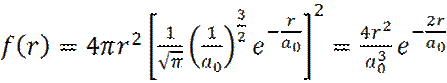(18)
Найдем экстремум функции f(r) :
(19)
В точке экстремума производная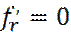 
.. Отсюда имеем:
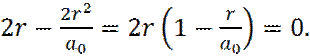(20)
Или
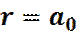(21)
Таким образом, наиболее вероятный радиус орбитали электрона в атоме водорода, в основном состоянии, совпадает с боровским радиусом a0 (радиусом первой орбиты Бора).
|
|
|
