 |
6. 12. Пробные смещения. Контрольное задание на применение метода монте-карло. Глава 7. метод молекулярной динамики для моделирования наносистем
|
|
|
|
6. 12. Пробные смещения
Рассмотрим поступательные смещения. Вполне приемлемый метод для создания пробного смещения заключается в добавлении случайных чисел из интервала: от - ∆ /2 до + ∆ /2, к x, y, z - координатам частиц (центров масс молекул):
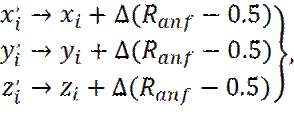 (23)
(23)
где Ranf – случайные числа, равномерно распределенные на интервале от 0 до 1.
Контрольное задание на применение метода Монте-Карло.
Записать алгоритм определения числа «пи», с использованием метода Монте-Карло.
Глава 7. МЕТОД МОЛЕКУЛЯРНОЙ ДИНАМИКИ ДЛЯ МОДЕЛИРОВАНИЯ НАНОСИСТЕМ
7. 1. Моделирование методом молекулярной динамики
Моделирование методом молекулярной динамики во-многом похоже на реальный эксперимент.
Во-первых, готовится образец материала, свойства которого мы собираемся изучить. Далее подбирается модель системы из N частиц.
Наконец, решаются уравнения движения Ньютона, для исследуемой системы, до тех пор, пока свойства системы не перестают меняться, с течением времени (приводим систему к равновесию).
После достижения равновесия мы приступаем к фактическим расчетам интересующих величин.
При расчете наблюдаемой макровеличины, на основе метода молекулярной динамики, необходимо уметь выразить эту наблюдаемую величину, как функцию положения, и импульса частиц, в системе.
Например, подходящим определением температуры, в системе многих тел, является определение, основанное на использовании положения о равнораспределении энергии, по всем степеням свободы, которые входят квадратично в гамильтониан системы (сумму кинетической и потенциальной энергий). В частности, для средней кинетической энергии на одну степень свободы имеем:
|
|
|
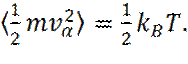 (1)
(1)
В моделировании, это уравнение используется, как рабочее определение температуры.
На практике имеет смысл рассчитывать полную кинетическую энергию системы и делить это значение на число степеней свободы
Nf = 3N – 3 для системы N частиц, при сохранении общего импульса, в системе. Так, как, полная кинетическая энергия системы флуктуирует, изменяется и мгновенное значение температуры:
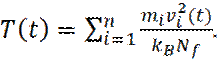 (2)
(2)
Относительные флуктуации температуры имеют порядок 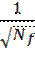 .
.
Учитывая что, как правило, Nf бывает порядка 102 - 103 , статистические
Флуктуации температуры составляют порядка 5 – 10%. Для получения
точной оценки температуры необходимо проводить усреднение по большему
числу частиц.
7. 2. Алгоритм расчетов по методу молекулярной динамики
Алгоритм включает следующие этапы.
1. Задание параметров, определяющих условия, при которых производится моделирование (например, начальная температура, количество частиц, плотность, временной шаг и т. д. ).
2. Задаются начальные положения частиц и их скорости.
3. Рассчитываются силы, действующие на все частицы в системе.
4. Проводится интегрирование уравнений движения Ньютона. Этот шаг вместе с предыдущим составляет основу моделирования. Они повторяются до тех пор, пока не завершится расчет эволюции системы во времени на интересующем нас временном интервале.
5. После окончания главного цикла, вычисляются и выводятся средние значения рассчитываемых величин и происходит завершение программы.
Рассмотрим теперь более подробно отдельные этапы алгоритма.
7. 3. Задание начальных значений параметров и положения частиц (инициализация)
Чтобы инициировать процесс моделирования необходимо задать начальные положения и скорости всех частиц в системе. Положения частиц должны быть выбраны совместимыми со структурой, которую мы стремимся воспроизвести.
|
|
|
В любом случае частицы должны располагаться так, чтобы не было заметного перекрывания атомов и молекул. Часто это достигается за счет первоначального размещения частиц в узлах кубической решетки.
Для задания начальных значений скоростей, каждой компоненте скорости, у каждой частицы, приписывается произвольное значение, с равномерным распределением, в интервале [- 0, 5; 0, 5].
атем производится сдвиг значений скоростей таким образом, чтобы суммарный импульс в системе стал равным нулю, а также проводится перемасштабирование скоростей для достижения желаемого значения средней кинетической энергии.
В состоянии теплового равновесия выполняется следующее соотношение
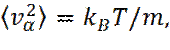 (3)
(3)
где vα - α -я компонента скорости частицы.
Соотношение (3) может быть использовано для определения мгновенной температуры T(t), в момент времени t:
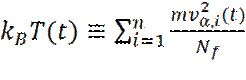 (4)
(4)
Очевидно, что возможно подогнать значение мгновенной температуры T(t), к желаемому значению T, путем перемасштабирования всех скоростей, с коэффициентом 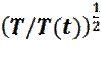 .
.
Значения скоростей сами по себе не используются при решении уравнений Ньютона.
Для предсказания положения частиц на следующем шаге используются положения частиц, в настоящий (X) и предыдущий (Xm) моменты времени, вместе с информацией о силах (f), действующих на частицу.
В начале моделирования, для нормального выполнения алгоритма,
необходимо искусственно задать положения частиц в предыдущий момент
времени.
Ограничиваясь учетом только закона сохранения импульса, можно оценить предыдущее положение частиц как:
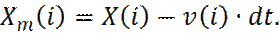 (5)
(5)
|
|
|


