 |
7.4. Расчет сил. 7.5. Пример расчета сил взаимодействия в Леннард-Джонсовской жидкости. 7.6. Интегрирование уравнений движения
|
|
|
|
7. 4. Расчет сил
Расчет сил, действующих на каждую частицу, является наиболее трудоемким этапом моделирования методом молекулярной динамики.
Если рассматривать модель системы с парными аддитивными взаимодействиями, необходимо учитывать вклад всех соседей рассматриваемой частицы. Если же рассматривать только взаимодействие между некоторой частицей и ближайшим образом другой частицы (периодические граничные условия), то для системы N частиц, необходимо вычислить N·(N-1)/2, парных взаимодействий.
Первоначально, необходимо рассчитать текущее расстояние в направлении x, y, z, для каждой пары частиц. Пусть это расстояние xr .
При расчете межмолекулярных взаимодействий, с периодическими граничными условиями, используют обрезку потенциала, на расстоянии rc (где rc должен быть меньше половины диаметра периодической ячейки).
В этом случае мы всегда можем свести расчет межмолекулярных взаимодействий между молекулами i и j, к взаимодействию между молекулой i, и ближайшим периодическим образом молекулы j.
В случае использования простой кубической ячейки, с периодическими
граничными условиями, расстояние в любом направлении, между i и ближайшим периодическим образом, молекулы j, всегда должно быть меньше (по абсолютной величине), чем половина диаметра периодической ячейки.
Удобный способ вычислить расстояние между i и ближайшим периодическим образом j, заключается в использовании функции ближайшего целого, nint(x), которая округляет реальное число x, до ближайшего целого. Так, имея расстояние по x, между молекулами i и j, равное xr, расстояние, по x, между i, и ближайшим образом j, вычисляется как:
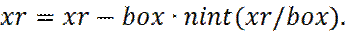 (6)
(6)
|
|
|
гдеbox – диаметр периодической ячейки.
Вычислив, таким образом, все декартовы составляющие вектора расстояния rij, между i и ближайшим периодическим образом j, определяется величина rij2.
Далее проверяется будет ли rij2 меньше квадрата радиуса обрезки rc2.
Если нет, то сразу же производится переход к следующему значению.
Если какие-либо две частицы расположены достаточно близко, чтобы они могли взаимодействовать друг с другом, тогда требуется рассчитать силы
между этими частицами, а также вклад в потенциальную энергию.
При этом, необходимо знать выражение для потенциальной энергии взаимодействия двух частиц, на расстоянии r.
Так, x -составляющая силы fx(r), будет выражаться через потенциальную энергию взаимодействия u(r), в виде:
 (7)
(7)
Рассмотрим пример взаимодействия молекул в неполярной жидкости.
Энергия взаимодействия двух частиц в ней описывается потенциалом Ленард- Джонса (1924 год):
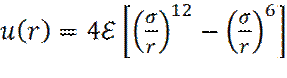 (8)
(8)
В уравнении (8) ε –глубина потенциальной ямы; σ – расстояние, на котором
энергия взаимодействия становится равной нулю.
7. 5. Пример расчета сил взаимодействия в Леннард-Джонсовской жидкости
Выведем выражение для x -составляющей силы взаимодействия молекул,
на расстоянии r.
Введем безразмерные координаты: 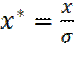 ,
, 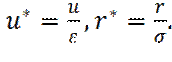
В новых переменных потенциал Леннард-Джонса примет вид:
 (9)
(9)
Теперь x -составляющая силы взаимодействия fx молекул будет равна:
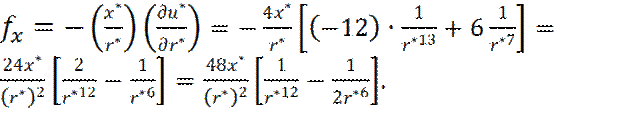 (10)
(10)
7. 6. Интегрирование уравнений движения
После того, как все силы между частицами рассчитаны, можно проводить интегрирование уравнений движения Ньютона. Для этого разработаны различные алгоритмы. Рассмотрим распространенный алгоритм Верле.
Для вывода алгоритма, разложим координаты частицы r(t+Δ t), в момент времени, t+ Δ t, в ряд Тейлора
 (11)
(11)
аналогично:
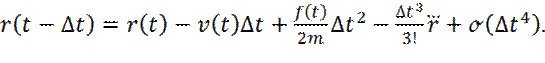 (12)
(12)
Суммируя два последних уравнения, получаем:
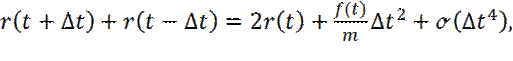 (13)
(13)
Или
 (14)
(14)
Погрешность уравнения (14) имеет порядок Δ t4 (где Δ t – шаг интегрирования по времени).
|
|
|
Алгоритм Верле позволяет получить и выражение для скорости частиц
v(t), в момент времени t. Для этого вычтем уравнение (12) из уравнения (11):
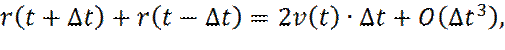 (15)
(15)
Откуда:
 (16)
(16)
Этим методом значения скоростей могут быть получены лишь с точностью
до Δ t2.
После вычисления новых координат частиц, можно отбросить значения координат в момент t – Δ t. Текущие координаты теперь рассматриваются, как предыдущие, а только что рассчитанные новые координаты рассматриваются, как текущие.
После каждого шага, по времени, вычисляется текущая температура, текущее значение потенциальной энергии (вычисляется вместе с расчетом сил) и полная энергия. При этом полная энергия должна сохраняться.
|
|
|


