6.1.1. Примеры применения метода Монте-Карло. Вычисление определенного интеграла по методу Монте-Карло

6. 1. 1. Примеры применения метода Монте-Карло. Вычисление определенного интеграла по методу Монте-Карло

 

1. Вычисление определенного интеграла .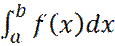

Традиционно при численном интегрировании отрезок [a, b] делится на равномерно распределенные узлы. Вычисляется f(x) в этих узлах и производится суммирование.

        Согласно методу Монте-Карло рассматривают случайную величину u, равномерно распределенную на отрезке [a, b]. Тогда функция f(u) также будет случайной величиной и ее математическое ожидание

E f(u) будет:

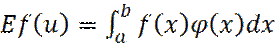   (1)

где φ (x) - функция плотности распределения случайной величины u, равная:

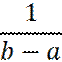
Следовательно, получаем:

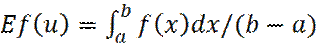   (2)

Откуда:

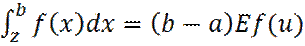   (3)

Но математическое ожидание E[f(u)] легко смоделировать, организовав случайный процесс и вычислив выборочное среднее. Таким образом вычисление определенного интеграла по методу Монте-Карло будет включать.

1. С использованием датчика случайных чисел с равномерным распределением на [a, b] образуем N значений случайной величины u.

2. Вычисляем значения случайной функции f(u_i) в точке u_i.

3. Вычисляем выборочное среднее

   (4)

4. Вычисляем искомый интеграл:

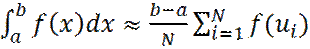   (5)

6. 1. 2. Геометрическая интерпретация метода Монте-Карло для численного интегрирования функций

Пусть требуется определить площадь под графиком функции f(x) (рис. )

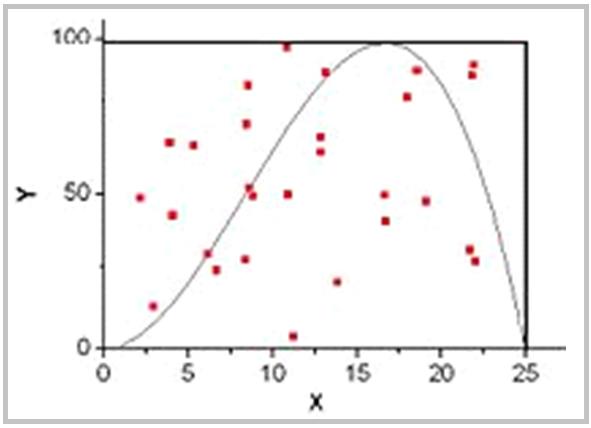
Для определения площади под графиком используем следующий стохастический алгоритм.

1. Ограничим функцию прямоугольником (n-мерным параллелепипедом в случае n измерений), площадь которого S можно легко вычислить. Причем, любая сторона должна содержать хотя бы 1 точку графика.

2. Случайным образом размещаем точки в прямоугольнике ( N штук).

3. Определяем число точек, попавших под график функции ( K штук).

4. Площадь S_k  под кривой дается выражением

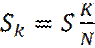   (6)

6. 2.  Моделирование наносистем методом Монте-Карло

Одной из основных задач моделирования наносистем является вычисление макросвойств системы, в качестве которых выступают термодинамические средние величины.

    Пусть требуется оценить макросвойство A, замкнутой равновесной системы из N частиц, находящихся в объеме V, при температуре T. Из статистической механики известно, что в качестве оценки макросвойства A выступает средняя величина ‹A›:

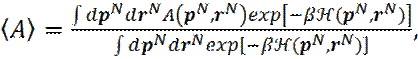   (7)

где 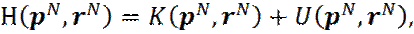 - гамильтониан системы, равный сумме кинетической и потенциальной энергий системы), r^N  – координаты частиц, p^N  – импульсы частиц, .

Так как кинетическая энергия является квадратичной функцией импульсов (K=p²/2m), то интегрирование по импульсам делается аналитически, а интегрирование по координатам частиц провести аналитически не удается. В связи с этим, необходимо применение численных методов.

Применение квадратурных методов вычисления, координатных интегралов невозможно из-за баснословно огромного количества вычислений:

если число частиц N=100, размерность пространства 3, и число узлов разбиения, по каждой координате 5, то количество расчетов составит

5^{3∙ 100} =10²¹⁰.

Такое количество вычислений выполнить невозможно и нужно искать другой метод. Следует отметить, что больцмановский фактор в определении средней величины

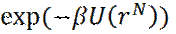   (8)

где:                                             

является резко меняющейся функцией координат и, в большинстве узлов, он близок к нулю. Это обстоятельство используется в методе Монте-Карло (метод статистических испытаний), модифицированном в 1953 году исследователем Метрополисом.

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: