 |
6.3. Метод Монте-Карло. Выборка по значимости
|
|
|
|
6. 3. Метод Монте-Карло. Выборка по значимости
В основе метода Метрополиса лежит идея «выборки по значимости», т. е. при вычислении интегралов в уравнении (7) делать расчет подынтегральной функции, только в тех точках rN, где больцмановский фактор (8) отличается от 0 (или близкой к нулю величины).
Это так называемая выборка по значимости.
Как уже отмечалось, в силу огромного количества вычислений невозможно рассчитать с помощью прямой (полной) выборки метода Монте-Карло конфигурационный интеграл вида:
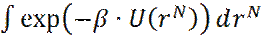(9)
Однако во многих случаях нужно вычислить не конфигурационную часть статистической суммы, а средние значения наблюдаемых величин:
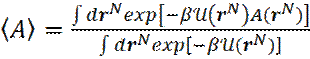. (10)
То есть на самом деле надо вычислить не сами интегралы (что почти
невозможно! ), а только их отношение.
Обозначим через Z конфигурационную часть статистической суммы:
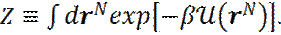(11)
Отношение exp(- β U(rN))/Z - есть функция плотности распределения частиц по потенциальным энергиям в системе.
Обозначим эту функцию плотности через N(rN):
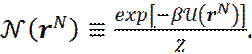(12)
Ясно, что генерация точек в конфигурационном пространстве должна
соответствовать этой функции плотности (12), так как при этом не будет рассматриваться область с малым вкладом в оценку < A> (и во-много раз сократится объем вычислений).
6. 4. Графическая интерпретация метода Метрополиса
Пусть требуется измерить (определить) среднюю глубину реки Нил.
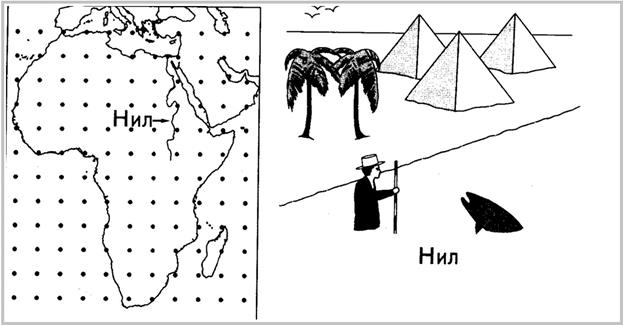
Будем сравнивать два способа определения средней глубины реки: обычное численное интегрирование, при котором вся поверхность разбивается точками, в которых определяется глубина воды, осуществляется суммирование и полученная сумма делится на число точек и с использованием выборки точек по Метрополису, т. е. построения взвешенного по значимости случайного блуждания, при котором точки размещаются в части пространства, где подынтегральная функция не является пренебрежимо малой (есть вода).
|
|
|
Таким образом, при использовании выборки по Метрополису мы будем двигаться вдоль реки, а не по всему пространству Африки.
В этом случайном блуждании пробный шаг отклоняется, если он выводит нас из воды, и принимается в других случаях. После каждого пробного смещения (принято оно или нет) измеряется глубина реки. Простое среднеарифметическое значение всех этих измерений дает оценку средней глубины Нила. В этом сущность метода Метрополиса.
6. 5. Создание точек в конфигурационном пространстве на основе больцмановского фактора
Сначала надо приготовить систему в конфигурации rN , обозначив ее буквой O (от old). Причем, больцмановский фактор ее exp(- β U(O)) не должен быть слишком малым.
Далее, добавляя небольшие случайные смещения Δ, к старой конфигурации O, мы создаем новую конфигурацию r‘ N, которую обозначим буквой n (от new).
Больцмановский фактор этой пробной конфигурации есть exp(- β U(n)).
Теперь надо решить, следует ли нам принять или отклонить пробную конфигурацию.
Введем понятие вероятности перехода системы из конфигурации O в
конфигурацию n : π (O → n). Элементы матрицы π должны удовлетворять
очевидному условию: они не должны разрушать достигнутое равновесие, т. е. в равновесии среднее число принятых переходов из состояния O, в любое другое состояние n, точно компенсируется числом обратных переходов:
(13)
6. 6. Структура шага метода Монте-Карло
Шаг метода Монте-Карло состоит из двух этапов. Во-первых, осуществляется процесс пробного перемещения из состояния «О» в состояние «n». Матрицу перехода, которая определяет вероятность реализации пробного перемещения из «О» в «n» обозначим через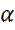 
(о→ n) ( 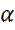обычно называют базовой матрицей марковской цепи).
|
|
|
Вторым этапом является решение о принятии или отклонении этого пробного перемещения. Обозначим вероятность принятия пробного перемещения из «о» в «n» через acc(o→ n). Очевидно, что
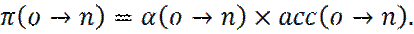(14)
Матрица 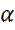часто принимается симметричной. Тогда с учетом условия (13), в равновесии будем иметь:
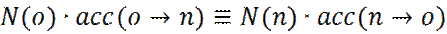(15)
Или:
(16)
6. 7. Вероятность принятия шага ACC(O→ N) и вероятность перехода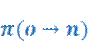 
В методе Метрополиса вероятность acc(o→ n) принятия шага o→ n равна:
.
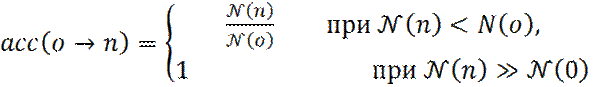Таким образом, в итоге, в схеме Метрополиса, вероятность перехода из состояния o, в состояние n, имеет вид:
|
|
|
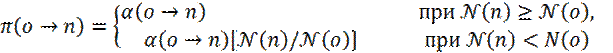
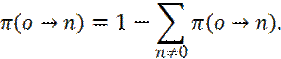
