5.9. Дисперсия радиуса орбитали электрона в атоме водорода в основном состоянии 1S

5. 9. Дисперсия радиуса орбитали электрона в атоме водорода в основном состоянии 1S

 

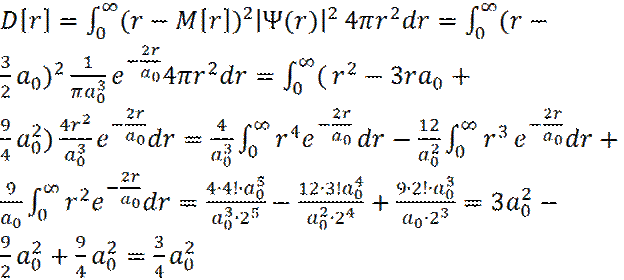   (23)

5. 10.  Многоэлектронные атомы. Метод Хартри-Фока.

 

Водородоподобные атомы являются единственными атомными системами, для которых могут быть получены точные волновые функции путем решения уравнения Шредингера. Уже для следующего за водородом элемента гелия возникают непреодолимые трудности. Смысл их становится понятным из рассмотрения оператора полной энергии атома гелия, в котором в поле ядра с зарядом Z= +2, находятся 2 электрона.

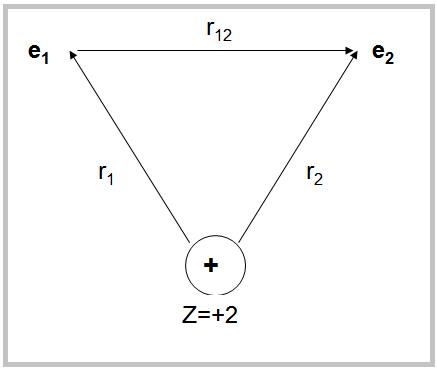
Рисунок. Координаты электронов e₁, e₂  в атоме гелия.

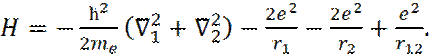   (24)

 

Гамильтониан H в уравнении (24) для атома гелия содержит последний член, отвечающий за межэлектронное отталкивание. Его величина зависит от координат обоих электронов r₁₂ =│ r₁ – r₂│, что не позволяет разделить переменные. По этой причине точное аналитическое решение уравнения Шредингера с гамильтонианом (24) невозможно.

    Гамильтониан многоэлектронного атома с n электронами и зарядом ядра Z имеет следующий вид:

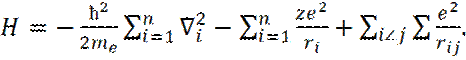   (25)

Первый член в уравнении (25) – оператор кинетической энергии электронов, второй – оператор потенциальной энергии электронов с ядром, третий – оператор энергии межэлектронного отталкивания.

Для более сложных атомов, с несколькими электронами, необходимо учитывать энергию отталкивания всех электронов. В 1927 году Д. Хартри предложил представить взаимодействие электрона со всеми остальными электронами, как его взаимодействие с усредненным полем, создаваемым ядром и остальными электронами. Это позволило заменить в уравнении (25) последний член, зависящий от координат двух электронов, функцией координат каждого отдельного электрона. Полная волновая функция атома Ψ, в этом случае, представлялась, как произведение волновых функций отдельных электронов:

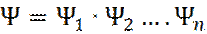   (26)

Последнее соотношение означает независимость движения электронов друг от друга.

Применяя вариационный метод Хартри, на основе уравнения (25), получил одноэлектронное уравнение, типа:

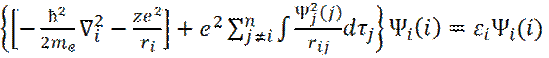(27)

где dτ – элементарный объем; ε _i – соответствует энергии электрона на i-ой орбитали атома с гамильтонианом Хартри (в фигурных скобках). Последний член в фигурных скобках соответствует эффективному потенциалу, представляющему собой усредненное электростатическое взаимодействие i-го электрона со всеми остальными электронами.

В. А. Фок усовершенствовал метод Хартри, добавив в уравнение (27) дополнительный член, учитывающий наличие, так называемой «обменной энергии», суть которой заключается в том, что два электрона, с параллельными спинами, не могут находиться в одной точке пространства, и это будет менять электростатическую энергию их отталкивания.

    В заключение следует отметить, что метод Хартри-Фока сводится к

аппроксимации точного электронного гамильтониана H, суммой одноэлектронных операторов (операторов Фока):

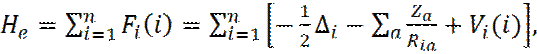 (28)

где значения V_i(i) определяется средним электростатическим полем, которое

действует на каждый электрон i, со стороны всех остальных электронов системы.

Глава 6. МЕТОД МОНТЕ-КАРЛО  ДЛЯ МОДЕЛИРОВАНИЯ НАНОСИСТЕМ

6. 1. Метод Монте-Карло. Определение

Метод Монте-Карло – это метод статистических испытаний, основанный на проведении большого числа реализаций случайного процесса, сформированного таким образом, чтобы получаемые вероятностные характеристики совпадали с искомыми решениями задачи.

    Метод предложен Метрополисом и Уламом в 1949 году.

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: