 |
7. 7. Применение метода молекулярной динамики для моделирования процесса диффузии
|
|
|
|
7. 7. Применение метода молекулярной динамики для моделирования процесса диффузии
Диффузия обусловлена молекулярным движением частиц жидкости (газа). На макроскопическом уровне диффузия описывается законом Фика, согласно которому, поток j диффундирующих частиц, пропорционален градиенту концентрации частиц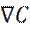 
, этого типа, со знаком минус
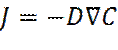(17)
где D – коэффициент диффузии;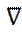 
- оператор «набла» (соответствует градиенту).
Рассмотрим моделирование процесса диффузии (самодиффузии), с позиций метода молекулярной динамики. Пусть в объеме жидкой фазы наносится возмущение индикатором, в виде δ -функции Дирака.
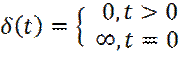(18)
Реально, это означает, что в момент времени t = 0, в центре объема, был импульсно введен индикатор, с бесконечно высокой концентрацией.
С макроскопической точки зрения, для описания эволюции частиц индикатора, необходимо привлечь закон сохранения массы частиц индикатора
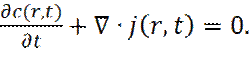(19)
и объединить его с законом Фика (17). Тогда получим
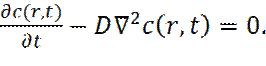(20)
Решая уравнение (20) с начальным условием:
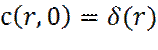(21)
где δ (r) – дельта функция Дирака, получаем:
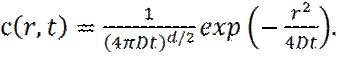(22)
Здесь d – обозначает размерность системы.
На самом деле, нас интересует применение метода молекулярной динамики, для оценки макроскопического параметра процесса молекулярной диффузии – коэффициента диффузии D.
Попытаемся связать эволюцию распределения во времени концентрации индикатора, с коэффициентом диффузии D (макропараметром процесса).
Если ввести понятие нормированной концентрации индикатора C(r, t), как:
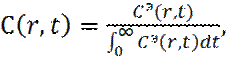(23)
то последняя будет являться функцией плотности распределения частиц индикатора по времени, на расстоянии r, от точки ввода индикатора (здесь C э(r, t) – размерная экспериментально замеряемая концентрация индикатора).
|
|
|
Тогда справедливо следующее равенство:
(24)
где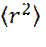 
- математическое ожидание (среднее значение) квадрата радиуса, продиффундировавших частиц индикатора.
Умножим теперь левую и правую части уравнения (20) на r2 и проинтегрируем по всему пространству:
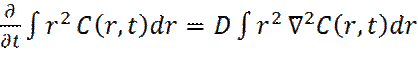(25)
Левая часть уравнения (25) равна: 
Применяя интегрирование по частям к правой части уравнения (25), получаем:
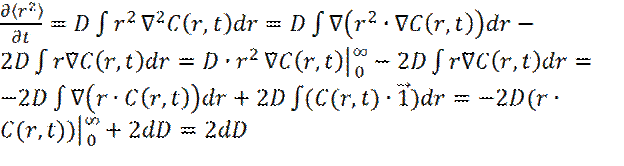(26)
Уравнение (26) устанавливает связь между коэффициентом диффузии D и шириной профиля концентрации индикатора. Это соотношение впервые было получено Эйнштейном. Коэффициент диффузии D является макроскопическим коэффициентом переноса, а ‹r2(t)› имеет микроскопическую интерпретацию: это средний квадрат расстояния, на которое сместились молекулы индикатора, за интервал времени t.
Это сразу же дает подсказку, как рассчитать D, методом молекулярной динамики. Надо для каждой частицы i рассчитать ее смещение Δ ri (t), за время t, и построить средний квадрат этих смещений, по всем частицам, в зависимости от времени t:
(27)
Тангенс угла наклона этой зависимости, при достаточно больших t , равен 2dD.
7. 8. Связь автокорреляционной функции скорости с коэффициентом диффузии (соотношение Грина-Кубо)
Получим выражение, связывающее коэффициент диффузии D, со скоростями частиц vi (t). За основу возьмем соотношение:
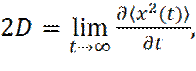(28)
и для простоты будем рассматривать средний квадрат смещения только по одной из декартовых координат. Следует уточнить, что под смещением частицы в системе, с периодическими граничными условиями, подразумевается интеграл по времени от скорости, выделенной частицы
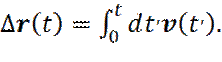(29)
Если записать смещение частицы x(t), за время t, как интеграл по времени от x -составляющей скорости выделенной частицы, получим:
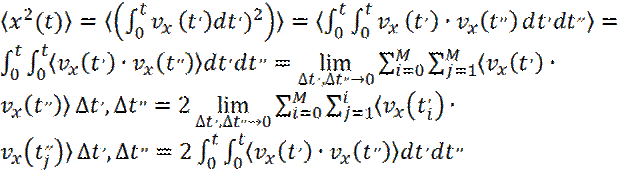(30)
|
|
|
Величина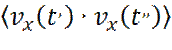 
называется автокорреляционной функцией скорости. Она показывает связь скорости, в различные моменты времени t’ и t’’.
Автокорреляционная функция скорости является равновесным свойством системы, потому что отражает связь между скоростями, осредненную по всем частицам, при движении системы частиц вдоль равновесной траектории. Поскольку равновесные свойства инвариантны относительно времени начала отсчета, автокорреляционная функция зависит только от разности (t’ – t’’). Следовательно, можно записать:
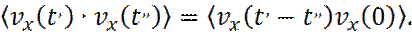(31)
Подставляя (31) и (30) в уравнение (29), получаем:
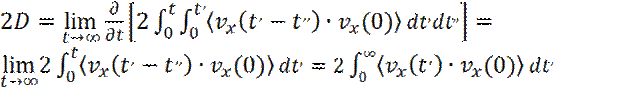(32)
Отсюда:
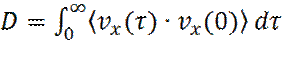(33)
Из последнего выражения видна связь коэффициента диффузии D, с интегралом от автокорреляционной функции скорости. Соотношение (33) называется соотношением Грина-Кубо.
Аналогичные соотношения Грина-Кубо существуют и для многих других кинетических коэффициентов, таких, как сдвиговая вязкость, теплопроводность, электропроводность и т. д.
Временные корреляционные функции могут быть легко рассчитаны, в ходе метода молекулярной динамики. Соотношение Грина-Кубо для D и соотношение Эйнштейна полностью эквивалентны.
|
|
|
