Виды средств диагностирования

 

 

Подсоединяются или работают совместно с контролируемым изделием только в момент контроля и не являются элементом изделия.

 

Тормозной стенд, стенд для проверки углов установки колес и др.

 

Приборы контроля состава отработавших газов, тестеры. и др.

 

 

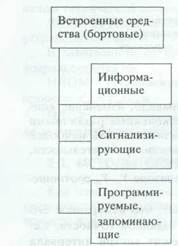
Являются конструктивным элементом автомобиля и осуществ­ляют контроль непрерывно или периодически по определенной программе.

 

Информируют о режимах работы и состоянии: температура агрегатов, скорость, частота вращения коленвала, давление масла и т.д.

Предупреждают о возможном наступлении предотказного состояния (Уп.д) или возникновении скрытых отказов: давле­ние масла, заряд аккумуляторной батареи.

Отслеживают и запоминают информацию о состоянии для считывания в стационарных условиях; поиск неисправности; самодиагностика; звуковая, визуальная, речевая информация о предотказном состоянии.

 

ак правило, используются два способа диагностирования. При первом в про­цессе диагностирования на объект диагностирования (ОД), не находящийся в рабо­чем состоянии, осуществляются определенные механические, электрические, гидравлические и другие воздействия и с помощью датчиков фиксируется его реакция в виде диагностического сигнала S_i.

При втором способе объект диагностирования выводится на заданный режим работы, и также с помощью датчиков от него воспринимаются сигналы, харак­теризующие диагностические параметры S_i. Эти сигналы преобразуются (модули­руются) в электрические, улучшаются (очищаются от "шума"), например, с по­мощью аналого-цифрового преобразователя и аналогового мультипликатора и далее поступают или непосредственно в средства отображения информации и считываются оператором, или, в более сложных диагностических приборах, в микропроцессор (микропроцессоры), где с учетом информации, содержащейся в блоке памяти (запоминающее устройство), осуществляется анализ, а в ряде случаев и прогноз, и полученная информация передается в средства отображения.

В блоке памяти может также содержаться информация о механике-диагносте, проводившем соответствующий контроль.

В ряде диагностических приборов на дисплее может выдаваться рекомендация по конкретному перечню работ, которые необходимо выполнить данному автомобилю.

В блоке памяти могут содержаться сведения о предыдущем контроле данного автомобиля, что позволяет проследить динамику изменения диагностических пара­метров и дать прогноз наработок до предельно допустимого и предельного значе­ний параметров технического состояния.

На практике прямой и диагностический методы взаимодействуют и дополняют друг друга. Надо уметь определить рациональные сферы их использования.

Главным критерием выбора метода является сравнение суммарных затрат на предупреждение, выявление и устранение отказов и неисправностей при использовании прямых и диагностических методов контроля технического состояния, а также продолжительности процедуры.

 

2.4. ЗАКОНОМЕРНОСТИ ИЗМЕНЕНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ

 

1. ВИДЫ ЗАКОНОМЕРНОСТЕЙ

 

Для предупреждения отказов и неисправностей, а также для определения их источников, предъявления рекламационных претензий изготовителю или продавцу изделия мало констатировать сам факт возникновения отказа или неисправности. Необходимо знать причины, механизмы их возникновения и проявления, а также влияние различных отказов элементов на работоспособность автомобиля в целом, т.е. на способность выполнять транспортную работу. Иными словами, необходимо знать закономерности изменения технического состояния.

Процессы в природе и технике (в том числе и при технической эксплуатации) могут быть двух видов: процессы, характеризуемые функциональными зависимостями, и случайные (вероятностные, стохастические) процессы.

Для функциональных процессов характерна жесткая связь между функцией (зависимой переменной величиной) и аргументом (независимой переменной величиной), когда определенному значению аргумента (аргументов) соответствует определенное значение функции. Например, зависимость пройденного пути от скорости и времени движения.

Случайные процессы происходят под влиянием многих переменных факторов, значение которых часто неизвестно. Поэтому результаты вероятностного процесса могут принимать различные количественные значения (т.е. наблюдается рассеивание, или вариация) и называются случайными величинами (СВ).

Случайные процессы могут быть описаны пучком кривых У_i(t)> характеризующих изменение технического состояния конкретных изделий 1,2,3,...,i,...,n (рис. 2.6) от их наработки t. Иными словами, случайный процесс Y(t) может быть

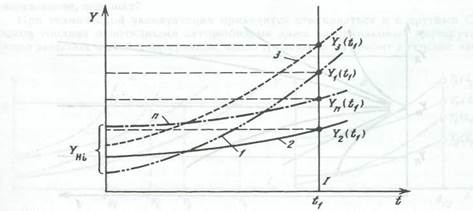
Рис. 2.6. Схема формирования случайного процесса

/ - сечение случайного процесса, Y₁-Y_n - случайные величины - реализация случайного процесса Y(t) при t = t₁,

описан функцией, которая при каждом новом значении аргумента характеризуется набором нескольких случайных величин. Конкретные значения случайной функции при фиксированном значении аргумента t называются реализацией случайной величины.

При эксплуатации в основном приходится иметь дело со случайными процессами и величинами.

 

описан функцией, которая при каждом новом значении аргумента характеризуется набором нескольких случайных величин. Конкретные значения случайной функции при фиксированном значении аргумента t называются реализацией случайной величины.

При эксплуатации в основном приходится иметь дело со случайными процесса­ми и величинами.

2. ЗАКОНОМЕРНОСТИ ИЗМЕНЕНИЯ ТЕХНИЧЕСКОГО СОСТОЯНИЯ АВТОМОБИЛЯ ПО ЕГО НАРАБОТКЕ (ЗАКОНОМЕРНОСТИ ТЭА ПЕРВОГО ВИДА)

У значительной части узлов и деталей процесс изменения технического состоя­ния в зависимости от времени или пробега автомобиля носит плавный, монотонный характер, приводящий к возникновению так называемых постепенных отказов. При этом характер зависимости может быть различным (рис. 2.7). В случае постепенных отказов изменение параметра технического состояния конкретного изделия или среднего значения для группы изделий аналитически достаточно хорошо может быть описано двумя видами функций:

целой рациональной функцией п-го порядка

 

 

 

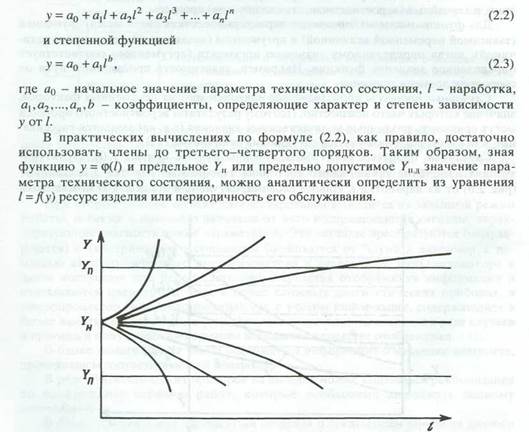
Рис. 2.7. Возможные формы зависимости параметра технического состояния Y от нара­ботки l

Y_н, Y_n - начальное и предельное значения параметра

смены работы поста ремонтной мастерской, станции ТО; число заездов на АЗС и др. Все это сказывается на нормировании и организации ТО и ремонта, опре­делении необходимых для этого ресурсов.

Для решения этих задач необходимо уметь оценивать вариацию СВ.

 

4. ОЦЕНКИ СЛУЧАЙНЫХ ВЕЛИЧИН

Рассмотрим простейшие методы оценки СВ. Исходные данные - результаты наблюдений за изделиями или отчетные данные, которые выявили индивидуальные реализации случайных величин (например, наработки на отказ, фактический расход топлива, материалов и т.д.).

1. Случайные величины (от 1 до п) располагают в порядке возрастания или убывания их абсолютных значений:

Точечные оценки позволяют предварительно судить о качестве изделий и технологических процессов. Чем ниже средний ресурс и выше вариация (о, v, z), тем ниже качество конструкции и изготовления (или ремонта) изделия. Чем выше коэффициент вариации показателей технологических процессов ТЭЛ (трудоемкость, простои в ТО или ремонте, загрузка постов и исполнителей и др.), тем менее совершенны применяемые организация и технология ТО и ремонта.

3. Вероятностные оценки СВ. При вероятностных оценках рекомендуется размах СВ разбить на несколько (как правило, не менее 5-7 и не более 9-11) равных по длине Δхинтервалов (табл. 2.4). Далее следует произвести группировку, т.е. определить число случайных величин, попавших в первый (п₁), второй (п₂) и остальные интервалы. Это число называется частотой. Разделив каждую частоту на общее число случайных величин (п₁ + п ₂+••• + п_n = п), определяют частость (ω_i = n_i/n. Частость является эмпирической (опытной) оценкой вероятности Р,

 

 

Таблица2.4 Пример вероятностной оценки СВ
Номер интервала J	Интервал Δx, тыс. км	Середина интервала Xi ТЫС. КМ	Число отказов ni в интер­вале	Частость (вероят­ность) ωi =pi	Оценка накопленных вероятностей
отказа F	безотказ­ности R
	6-8			0,06	0,06	0,94
	8-10			0,12	0,18	0,82
з	10-12			0,19	0,37	0,63
	12-14			0,25	0,62	0,38
	14-16			0,2	0,82	0,18
	16-18			0,13	0,95	0,05
	18-20			0,05	1,00
Всего	-	-		1,00	-	-

т.е. при увеличении числа наблюдений частость приближается к вероятности: ^ю/ ~* Pi- Полученные при группировке СВ результаты сводятся в таблицу (см. табл. 2.4), данные которой имеют не только теоретическое, но и практическое значение. Например, по результатам наблюдений можно предположить, что у аналогичных изделий в тех же условиях эксплуатации и в интервале наработ­ки 6-8 тыс. км может отказать около 6% изделий ω_i ~ Р_i = 0,06), в интервале 8-10 тыс. км - 12%, интервале 10-12 тыс. км - 19% и т.д.

Следовательно, имея систематизированные данные по отказам, можно прогнозировать и планировать число воздействий (программу работ), потреб­ности в рабочей силе, площадях, материалах и запасных частях.

4. Вероятность случайного события. В общем виде это отношение числа слу­чаев, благоприятствующих данному событию, к общему числу случаев.

 

 

Обычно применяется следующая буквенная индексация рассмотренных собы­тий и понятий:

F (failure) - отказ, авария, повреждение, вероятность этих событий;

R (reliability) - безотказность, надежность, прочность, вероятность этих событий;

Р (probability) - вероятность.

Вероятность отказа может быть получена также последовательным суммиро­ванием интервальных вероятностей за наработку X, т.е.

F(x) = p_l+p₂ +... + p_j,

где j— номер интервала, соответствующий наработке X.

5. Следующей характеристикой случайной величины является плотность вероятности (например, вероятности отказа) /(х) - функция, характеризующая вероятность отказа за малую единицу времени при работе узла, агрегата, детали без замены. Если вероятность отказа за наработку F(x) = m(x)/n, то, дифферен­цируя ее при п = const, получим плотность вероятности отказа

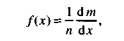
где dm/dx - элементарная "скорость", с которой в любой момент времени проис­ходит приращение числа отказов при работе детали, агрегата без замены.

 

 

Если организаторы производства без технико-экономического анализа назна­чали периодичность, например, /_то = 10 тыс. км (см. табл. 2.4), то примерно 18 из­делий из 100 (Я| = 6 и «₂ = 12, т(х) = 18) откажут ранее назначенного ТО, т.е. веро­ятность отказа

Остальные 82% изделий (19 + 25 + 20+13 + 5) имеют потенциальную наработ­ку на отказ дс, > 10 тыс. км. Следовательно, ТО им будет произведено ранее, чем они могут отказать, и вероятность их безотказной работы

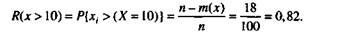
Для первых отказов невосстанавливаемых изделий и взаимно дополняющих событий (отказ - работоспособное состояние) имеет место условие F(x) + R(x) = = 0,18 + 0,82= 1, т.е., зная вероятность отказа, можно определить вероятность безотказной работы и наоборот.

7. Используя данные табл. 2.4, можно также определить некоторые точечные
оценки СВ.

Среднее значение СВ

где j - номер интервала.

Для данных табл. 2.4 имеем:

J = 7-0,06 + 9-0,12 +11-0,19 +13-0,25+15-0,20+17-0,13 +19-0,05 = = 13,0 тыс. км.

Таким образом, если бы периодичность ТО равнялась средней наработке на отказ, то более 60% изделий в рассматриваемом примере отказали бы до обслуживания.

Среднеквадратическое отклонение

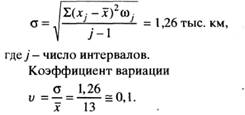
8. Важным показателем надежности является интенсивность отказов Х(х) -
условная плотность вероятности возникновения отказа невосстанавливаемого
изделия, определяемая для данного момента времени при условии, что отказа до
этого момента не было. Аналитически для получения к(х) необходимо элементар­
ную вероятность dm/dx отнести к числу элементов, не отказавших к моменту д:, т.е.

 

 

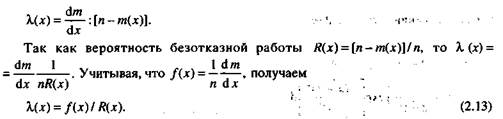
Это универсальная формула определения вероятности безотказной работы не-восстанавливаемого элемента для любого закона распределения. Зная интенсив­ность отказов, можно для любого момента времени или пробега определить вероятность безотказной работы. Существуют внезапные и постепенные отказы (рис. 2.9). Последние описывают работу так называемых стареющих элементов.

9. Наглядное представление о величине и вариации СВ дает их графическое
изображение: гистограммы (/, рис. 2.10) и полигоны (2, рис. 2.10) распределения, а
также интегральные функции распределения вероятностей отказа (5, рис. 2.10) и
безотказной работы (4, рис. 2.10) и дифференциальные функции или законы рас­
пределения случайной величины (рис. 2.11).

10. В ряде случаев законы распределения случайных величин могут быть опи­
саны аналитически, как функции параметров этих законов. Такие аналитические
зависимости имеются для нормального, экспоненциального и ряда других законов
распределения СВ, описывающих процессы ТЭА.

Общий вид закона распределения:

Для процессов технической эксплуатации и непрерывных СВ наиболее харак­терны следующие законы распределения.

Нормальный закон распределения (двухпараметрический: о и х). Такой закон формируется, когда на исследуемый процесс и его результат влияет сравнительно большое число независимых (или слабозависимых) элементарных факторов (сла­гаемых), каждое из которых в отдельности оказывает лишь незначительное дейст­вие по сравнению с суммарным влиянием всех остальных.

 

 

Экспоненциальный закон (однопараметрический - X). При экспоненциальном законе распределения вероятность безотказной работы не зависит от того, сколько проработало изделие с начала эксплуатации, а определяется конкретной продол­жительностью рассматриваемого периода или пробега Ах, называемого временем выполнения задания. Таким образом, эта модель не учитывает постепенного изме­нения параметров технического состояния, например, в результате изнашивания, старения и других причин, а рассматривает так называемые нестареющие элемен­ты и их отказы. Экспоненциальный закон используется чаще всего при описании внезапных отказов, продолжительности разнообразных ремонтных воздействий и в ряде других случаев:

Закон распределения Вейбулла-Гнеденко проявляется в модели так называе­мого слабого звена. Если система состоит из группы независимых элементов, отказ каждого из которых приводит к отказу всей системы, то в такой модели рассмат­ривается распределение времени (или пробега) достижения предельного состояния системы как распределение соответствующих минимальных значений jc/ отдельных элементов:

 

 

Примером использования распределения Вейбулла-Гнеденко является рас­пределение ресурса подшипника качения. Этот ресурс ограничивается ресурсом одного из элементов (шарика, ролика, конкретного участка сепаратора и т.д.).

Значение аналитических зависимостей состоит в том, что если известен вид закона (на основе опыта, литературных источников, наблюдений) и его параметры, то можно расчетными методами, не проводя объемных наблюдений, воспроизвести (прогнозировать) ожидаемые вероятности отказов и других состояний изделий и процессов. Например, для нормального закона необходимо знать два параметра (i, о), a для экспоненциального - один (х или А,), чтобы рассчитать вероятность отказов и безотказной работы (приложение 5).

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: