Ряды динамики. Основные показатели рядов динамки. Методы выравнивая рядов динамики. Их применение в экономических расчетах.

Все явления природы и общества находятся в непрерывном движении и развитии. Статистика не могла бы правильно характеризовать все явления, если бы она не изучала их в развитии.

Процесс развития явления во времени называется динамикой.

Для отражения динамики явлений и процессов строят ряды динамики.

Ряд динамики – ряд изменяющихся во времени значений статистич. показателя, расположен. в хронологическ. порядке.

Динамика изучает закономерности развития, их рост или уменьшение, темпы роста или снижения. Каждое изменение, его величина или размеры характеризуются либо на определенный момент времени, либо за определенный промежуток времени в зависимости от этого могут быть моментными или периодическими (интервальными).

- моментные ряды – характеризуют явления или процесс на определенную дату или в определенный момент времени (у₀ – начальный уровень ряда, у_n – конечный уровень ряда). Примером могут служить данные о численности персонала фирмы по состоянию на первое число каждого месяца года.

- интервальные ряды – характеризуют явления и процессы за определенный период времени..

Средняя хронологическая моментного ряда равна сумме всех уровней ряда, поделенной на число членов ряда без одного, причем первый и последний члены ряда берутся в половинном размере.

Способы расчета средней арифметической зависят от вида динамического ряда:

- средняя хронологическая.

Каждый показатель ряда динамики называется уровнем (у).

Первый уровень ряда динамики называется – начальным, последний – конечным. Базисный уровень – у_0.

2. В завис-ти от расстояния между уровнями:

- равностоящие – ряды динамики следующих друг за другом периодов или след. через определ. промежуток.

- неравностоящие - если прерывающиеся периоды.

3. В зависимости от способа выражения уровней р.д.подразделяются на ряды абсолютные,атносительные и средние.

4.В завис-ти от наличия основной тенденции изучаемого процесса р.д. подразделяются на стандарционные и нестандарционные. Если математ. ожидание значения признака и дисперсия постоянны и не зависят от времени,то процесс считается стандарционным.

Средние показатели рядов динамики:

1. Для моментного ряда:

А) с равными промежутками

средняя хронологическая.

Б) с разными промежутками

2. Для интервального ряда:

а) с равными промежутками средняя ариф. простая

б) с неравными промежутками сред. ариф. взвешенная

 

Для анализа изменений явлений и процессов во времени определяют следующие показатели рядов динамики:

1. абсолютный прирост (∆у) – характеризует размер увеличения или уменьшения уровня ряда за определенный промежуток времени. Абсолютный прирост может определяться на базисной и цепной основе:

- базисная: ∆у = у_i – y₀

- цепная: ∆у = у_i – y_i-1

2. темп роста – определяется как отношение уровней рядов динамики. Темп роста показывает во сколько раз данный уровень ряда больше базисного (если данный коэф-т больше 100%) или какую часть базисного составляет текущий уровень за некоторый промежуток времени (если данный коэф-т меньше 1).

- базисный: Т_р = у_i/y₀ * 100%

- цепной: Т_р = у_i /y_i-1 *100%

3. темп прироста – характеризует относительную скорость изменения уровня ряда в единицу времени.

- базисный: Т_пр = ∆у/y₀ * 100%

- цепной: Т_пр = ∆у/y_i-1 *100%

Т_пр = Т_р – 1 – если темп роста в коэф-тах; Т_пр = Т_р – 100 – если темп роста в %.

4. абсолютное значение 1% прироста – представляет собой 1 сотую часть базисного уровня или это отношение абсолютного прироста к соответствующ. темпу прироста. Рассчитывается на цепной основе:

│%│= ∆у/ Т_пр = 0,01* y_i-1

5. средний уровень ряда динамики:

а) для моментных рядов: - с равностоящими уровнями определяется по средней арифметической простой; - с неравностоящими уровнями по средней хронологической взвешенной.

б) для интервальных рядов: - с равностоящими уровнями по средней арифметической простой; - с неравностоящими уровнями по средней арифметич. взвешенной.

6. абсолютный прирост:

7. средний темп роста: ; Тр – в коэф-тах.

а) для моментных рядов с равностоящими уровнями:

б) моментный ряд с неравностоящими уровнями:

в) интервальные ряды с равностоящ. уровнями:

г) интервальные ряды с неравностоящ. уровнями:

Средний уровень для моментных рядов с равно стоящими уровнями: =

Пример: определить среднюю численность работников в первом квартале, если численность работников была:

Дата 1.01 1.02 1.03 1.04

Число работников 34 33 32 40

= чел.

Моментный ряд с неравно стоящими уровнями:

Пример: определить среднюю численность работников за три квартала:

Дата 1.01 1.04 1.10

Число работников 30 31 40

= чел.

Интервальный ряд с равностоящими уровнями: = Пример:

Месяц Янв. Фев. Март

Выручка 300 310 380 = тыс. руб.

Интервальный ряд с неровно стоящими уровнями: =

Пример: определить выручку если известно:

Месяц Янв. Май. Сент. Дек.

Выручка 20 22 24 28 = 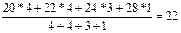тыс. руб.

Методы выравнивания рядов динамики.

Важнейшим условием правильного построения ряда динамики является сопоставимость всех входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.

Рассмотрим основные причины несопоставимости уровней ряда динамики.

Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения или единиц счета. Нельзя например сравнивать и анализировать цифры о производстве тканей, если за один год цифры даны в погонных метрах, а за другие – в квадратных метрах. На сопоставимость ряда динамики непосредственно влияет методология учета или расчета показателей. Например, если в одни годы среднюю урожайность считали в засеянной площади, а в другие с убранной, то такие уровни будут несопоставимы.

Условием сопоставимости уровней ряда динамики является периодизация динамики. – процесс выделения однородных этапов развития рядов динамики.

Важно также, чтобы в ряду динамики интервалы, или моменты, по которым определены уровни, имели одинаковый экономический смысл. Скажем, при изучении роста поголовья скота бессмысленно сравнивать цифры поголовья по состоянию на 1 октября с 1 января, так как 1я цифра включает не только скот, оставшийся на зимовку, но и предназначенный к убою, а вторая цифра включает только скот, оставшийся на зимовку.

Уровни ряда могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.

Несопоставимость уровней ряда может возникнуть вследствие изменения территориальных границ областей, районов и т д.

Прежде чем анализировать динамический ряд, надо, исходя из цели исследования, убедиться в сопоставимости уровней ряда и при отсутствии последней добиваться ее, пользуясь дополнительными расчетами.

Привидение уровней ряда к сопоставимому виду. Данный прием осуществляется методом смыкания рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых исчислены по разной методологии или разным территориальным границам. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).

Другой способ смыкания рядов динамики заключается в том, что уровни года, в котором произошли изменения принимаются за 100%, а остальные пересчитываются в процентах по отношению к этим уровням соответственно. В результате получаем сомкнутый ряд динамики.

Приведение рядов динамики к одному основанию. Та же проблема приведения к сопоставимому виду возникает и при параллельном анализе развития во времени экономических показателей отдельных стран, административных и территориальных районов. Это во-первых вопрос о сопоставимости цен сравниваемых стран, во-вторых о сопоставимости методики расчета сравниваемых показателей. В таких случаях ряды динамики приводятся к одному основанию, т.е. принимается за базу сравнения, а все остальные уровни выражаются в виде коэффициентов или в процентах по отношению к нему.

Пример

страна
Россия
Беларусь

Различные значения абсолютных уровней приведенных рядов динамики затрудняют выявление особенностей роста числа квартир в двух странах. Поэтому приведем абсолютные уровни рядов динамики к общему основанию, приняв за постоянную базу сравнения уровни 1996 г. Получим следующие данные.

Страна
Россия	100,0	92,1	80,5	70,5	77,4
Беларусь	100,0	121,1	126,3	89,5	102,3

В относительных величинах, выраженных в базисных темпах роста по каждой стране, несопоставимость уровней рядов динамики нивелируются. Различный характер развития выступает более наглядно.

Коэффициент опережения (замедления). Чтобы ответить на вопрос, во сколько раз число построенных квартир больше в Беларуси по сравнению с Россией, необходимо сравнить базисные коэффициенты роста за изучаемый период, т.е. вычислить коэффициент опережения (замедления) – Ко:

Ко=Т2/Т1, где (Т2>Т1) или Ко=Т1/Т2, где (Т1>Т2),

Эту формулу удобнее применять в том случае, когда ряд представляет постоянное повышение. Для рядов, где нет ярко выраженной тенденции к росту, удобнее за основание к приведению рядов брать средние показатели рядов динамики, в частности, средние темпы роста:

Ко=Т2/Т1,или Ко=Т1/Т2.

Для нашего примера средние темпы роста для Беларуси – 100,33%, для России – 96,41%. Таким образом, коэффициент опережения будет равен 1,04 раза (1,0033:0,9641), т.е. в 2000 г. по сравнению с 1996 г. число построенных квартир в Беларуси было в 1,04 раза больше, чем в России.

ПРИМЕР: Нейтрализация влияния объемного фактора на сумму затрат предпр

Вид прод	с/с прод, руб	Факт объем пр-ва,шт	Сумма затрат на факт объем пр-ва
пл	ф	По пл с/с	По факт с/с
А				300 (25*12000)	276 (23-12000)
Б				198 (6000*33)	204 (6000*34)
итог

 

в статистики применяют две группы методов: 1) Сглаживание или механическое выравнивание отдельных уровней ряда динамики с использование фактических значений соседних уровней. 2) Выравнивание с применением кривой проведённой между конкретными уровнями, таким образом, чтобы она отражала тенденцию присущую ряду и одновременно освободили его от незначительных колебаний. 3) Метод укрупнения интервалов – основан на укрупнении периода времени к которому относятся уровни. Уровни нового ряда могут быть получены путём суммирования исходного ряда, либо могут представлять средние уровни. 4) Распространённым приёмом при выявлении тенденции развития является сглаживание ряда динамики. Суть разных видов сглаживания сводится к замене фактических уровней ряда к расчётному, которые в меньшей степени подвержены колебаниям. Это способствует более чёткому проявлению тенденций развития явлений. 5) Метод скользящей средней. Данный метод заключается в том, что вычисляется средний уровень из определённого числа, первый по порядку уровней ряда. За тем средний уровень из такого же числа уровней ряда начиная со второго, далее начиная с третьего. Таким образом, при расчёте средних уровней они как бы «скользят» по ряду динамики от начала к концу ряда динами, каждый раз отбрасывая один пункт в начале и добавляя один следующий. Каждое звено скользящей средней – это средний уровень за соответствующий период, который относится к середине выбранного периода, если число уровней ряда динамики не чётное. Если число уровней ряда динамики чётное, то средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания. Чтобы ликвидировать такой вид, применяют способ центрирования, который заключается в нахождении средней из двух смежных скользящих средней для отнесения полученного уровня к определённой дате. При центрировании необходимо находить скользящие суммы, скользящие средние, не центрированные по этим суммам и средние из двух смежных не центрированных скользящих средних. 6) Аналитическое выравнивание – которое представляет собой уровни ряда динамики, выраженные в виде функции для отображения динамики ряда, в этом случае применяют различные функции (прямой, параболы).

 

⇐ Предыдущая34353637383940414243Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: