 |
Занятие 14. Тема: «Взаимное расположение прямой и плоскости». I. Контрольные вопросы и задания. II. Типовые задачи с решениями
|
|
|
|
Занятие 14
Тема: «Взаимное расположение прямой и плоскости»
Литература для самостоятельного изучения темы: [2], разд. I, гл. 3; [3], гл. 4; [4], гл. 4; [5], гл. II; [6], гл. II; [7], гл. 5; [8], гл. 5; [9], гл. 9; [10], гл. 10.
I. Контрольные вопросы и задания
1. Какой угол называется углом между прямой и плоскостью?
2. Напишите формулу нахождения синуса угла между прямой и плоскостью.
3. Найдите угол между прямой 
и плоскостью 
, если 
4. Напишите условие пересечения прямой и плоскости.
5. Как найти точку пересечения прямой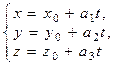 
с плоскостью 
6. Сформулируйте необходимый и достаточный признак параллельности прямой и плоскости.
7. Сформулируйте необходимый и достаточный признак перпендикулярности прямой и плоскости.
8. Напишите условие принадлежности прямой плоскости.
II. Типовые задачи с решениями
Задача 1. Найдите проекцию точки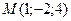 
на плоскость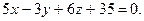 
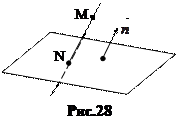
Решение. Этой проекцией является точка пересечения перпендикуляра к плоскости, проходящего через точку М. Для прямой, перпендикулярной плоскости, направляющим вектором будет 
(рис. 28).
Параметрические уравнения прямой, перпендикулярной плоскости и проходящей через точку М, примут вид: 
Подставляя эти значения в уравнение плоскости, находим:
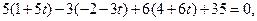
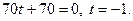
При этом значении t из параметрических уравнений прямой получаем: 
Следовательно, точка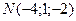 
– искомая проекция.
Ответ: 
Задача 2. Докажите, что прямая 
лежит в плоскости 
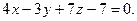
Решение. Найдем координаты направляющего вектора данной прямой: 
отсюда 
Вектор нормали плоскости равен 
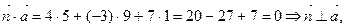значит, прямая либо параллельна плоскости, либо лежит в плоскости.
Найдем какую-либо точку прямой и проверим, лежит ли она в плоскости. Положив, например, 
из системы 
получаем 
Таким образом, точка 
прямой найдена. Подставляя ее координаты в уравнение плоскости, получаем верное равенство: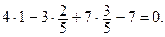 
|
|
|
Следовательно, данная прямая лежит в данной плоскости.
Задача 3. Составьте уравнение плоскости , проходящей через точку 
перпендикулярно к прямой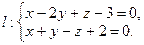 
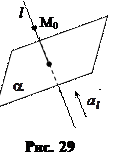
Решение. Так как 
то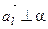 
(рис. 29).
Следовательно, плоскость задана точкой 
и вектором нормали 
Поэтому уравнение имеет вид: 
откуда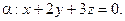 
Ответ: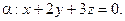
III. Задачи для упражнений
1. Докажите, что прямая 
параллельна плоскости 
2. Найдите точку пересечения прямой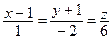 
и плоскости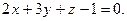 
3. Составьте уравнение прямой, проходящей через точку 
перпендикулярно к плоскости 
4. Составьте уравнение плоскости, проходящей через точку 
перпендикулярно к прямой 
5. При каком значении С прямая 
параллельна плоскости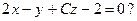 
6. При каких значениях l и C прямая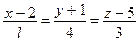 
перпендикулярна к плоскости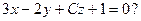 
IV. Задачи для самостоятельного решения
1. Составьте уравнение плоскости, проходящей через прямую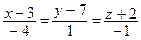 
перпендикулярно к плоскости 
2. Напишите уравнение плоскости, проходящей через параллельные прямые 
и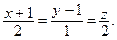 
3. Напишите уравнение перпендикуляра, опущенного из начала координат на прямую 
4. Составьте уравнение плоскости, проходящей через точку 
параллельно прямым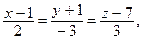 
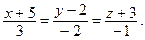
5. Составьте канонические уравнения прямой, которая проходит через точку 
параллельно плоскости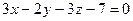 
и пересекает прямую 
6. Найдите точку Q, симметричную точке 
относительно прямой 
7. Найдите угол между прямой 
и плоскостью 
V. Задание на дом
1. Докажите, что прямая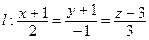 
параллельна плоскости 
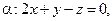а прямая 
лежит в этой плоскости.
2. Напишите уравнение плоскости, проходящей через прямую 
и точку 
3. Напишите уравнение плоскости, проходящей через прямую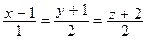 
и перпендикулярной плоскости 
4. Найдите угол между прямой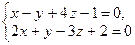 
и плоскостью 
|
|
|
5. При каких значениях А и В плоскость 
перпендикулярна к прямой 
|
|
|
