II. Типовые задачи с решениями

II. Типовые задачи с решениями

Задача 1. Какую поверхность определяет уравнение:

а) б) в)

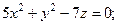г) д)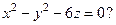

Найдите координаты вершин каждой из данных поверхностей.

Решение. Приведем каждое из уравнений а) – д) к каноническому виду:

а) Перепишем уравнение в следующем виде: 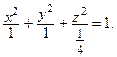 Это уравнение определяет эллипсоид вращения с полуосями  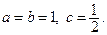Вершины эллипсоида имеют координаты:

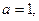
б)  – уравнение однополостного гиперболоида с полуосями  Вершины однополостного гиперболоида:

в) Разделим обе части уравнения на 4:  откуда  – уравнение двуполостного гиперболоида с полуосями  его вершины находятся в точках:

г) Разделим обе части уравнения на 7:  откуда получаем:  – уравнение эллиптического параболоида с осью Oz; его вершина находится в точке

д) Разделим обе части уравнения на 6: 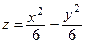 – уравнение гиперболического параболоида с осью Oz; его вершина находится в точке

Задача 2. Определите вид поверхности и изобразите эту поверхность:

а)       б)       в)

Решение. а) Приведем уравнение к каноническому виду: 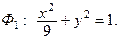 Это уравнение определяет эллиптический цилиндр. Чтобы изобразить эту поверхность, найдем уравнение ее направляющей  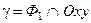и направление образующих.

Следовательно, направляющая 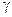 представляет собой эллипс, лежащий в плоскости  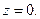Образующие цилиндра Ф₁ параллельны оси Oz.

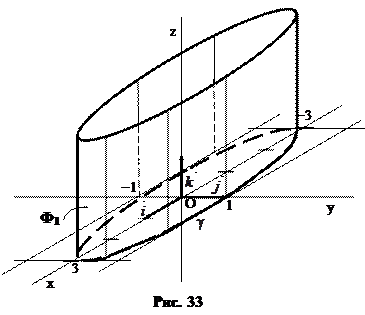
Строим сначала изображение направляющей 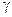, образующих, а затем изображаем цилиндр Ф₁ (рис. 33).

 

 

б) Приводим уравнение к каноническому виду: 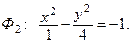 Это уравнение задает гиперболический цилиндр. Уравнение его направляющей  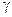имеет вид: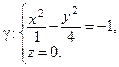

Следовательно, 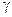 – гипербола с мнимой осью Ox, лежащая в плоскости  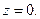Образующие параллельны оси Oz. Порядок построения изображения гиперболического цилиндра Ф₂ такой же, как в пункте а) (рис. 34).

в) Уравнение  определяет параболический цилиндр Ф₃. Его направляющая 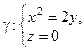   является параболой с осью Oy, лежащей в плоскости  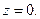Вершина параболы находится в точке  Чтобы построить параболу 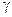, найдем координаты двух вспомогательных точек, принадлежащих параболе , в системе координат  и

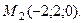
Параболический цилиндр Ф₃ изображен на рис. 35.

Задача 3. Определите вид поверхности Ф: 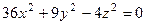 и изобразите эту поверхность.

Решение. Приведем уравнение поверхности Ф к каноническому виду, разделив обе части на 36:  Это уравнение определяет конус с вершиной в начале координат.

Чтобы построить эту поверхность, найдем сечение  этой поверхности плоскостью :    

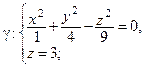
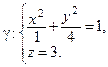
Следовательно,  – эллипс с полуосями , лежащий в плоскости , параллельной плоскости Oxy.

Построение изображения конуса Ф начинаем с построения изображения плоскости  и эллипса , затем достраиваем поверхность Ф (рис. 36).

 

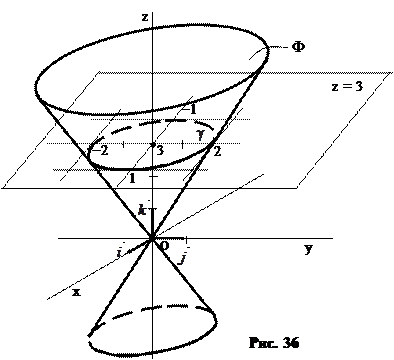
Задача 4. Изобразите поверхности: а) 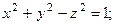    б)

Решение. а) Данное уравнение определяет однополостный гиперболоид Ф₁. Чтобы его изобразить, найдем сначала уравнения линий пересечения поверхности Ф₁ с координатными плоскостями Oxy и Oyz:

Следовательно,  – эллипс (точнее, окружность радиуса 1), лежащий в плоскости Oxy.

Следовательно,  – гипербола с мнимой осью Oz, лежащая в плоскости Oyz. Ее полуоси равны 1.

Порядок изображения поверхности Ф₁ таков (рис. 37):

1) Изображаем линию  (горловое сечение однополостного гиперболоида);

2) Изображаем линию

3) Изображаем однополостный гиперболоид Ф₁.

б) Данное уравнение определяет гиперболический параболоид Ф₂.

Найдем уравнения лини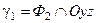й  и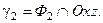

Следовательно, 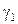 – парабола с осью Oz, лежащая в плоскости Oyz; ее ветви направлены в сторону, противоположную положительному направлению оси Oz.

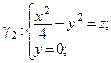
Следовательно, 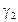 – парабола с мнимой осью Oz, лежащая в плоскости Oxz; ее ветви направлены в положительном направлении оси Oz.

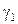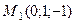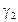Изображаем параболу , используя вспомогательные точки  и  (рис. 38). Изображаем параболу , используя вспомогательные точки  и  И, наконец, изображаем поверхность Ф₂ (рис. 38).

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: