 |
V. Задание на дом. Занятие 11. Тема: «Расстояние от точки до прямой. Направленный угол между двумя прямыми». I. Контрольные вопросы и задания
|
|
|
|
V. Задание на дом
1. Через точку пересечения прямых  и
и  проведите прямую, проходящую:
проведите прямую, проходящую:
а) через начало координат;
б) параллельно оси Ox;
в) параллельно оси Oy;
г) через точку М(7; –1).
2. Составьте уравнения прямых, проходящих через вершины треугольника 

 параллельно противоположным сторонам.
параллельно противоположным сторонам.
3. Даны последовательные вершины выпуклого четырехугольника A(–3; 1), B(3; 9), C(7; 6) и D(–2; –6). Определите координаты точки пересечения его диагоналей.
4. Даны две смежные вершины А(–3; –1) и В(2; 2) параллелограмма ABCD и точка Q(3; 0) пересечения его диагоналей. Составьте уравнения сторон этого параллелограмма.
5. Определите, при каком значении m две прямые пересекаются в точке, лежащей на оси абсцисс:  и
и 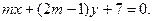
Занятие 11
Тема: «Расстояние от точки до прямой.
Направленный угол между двумя прямыми»
Литература для самостоятельного изучения темы: [1], гл. V; [2], разд. I, гл. 1; [3], гл. 1; [4], гл. 1; [5], гл. II; [6], гл. II; [7], гл. 5; [8], гл. 5; [9], гл. 3; [10], гл. 3.
I. Контрольные вопросы и задания
1. Дайте определение вектора нормали прямой.
2. Найдите вектор нормали прямой:
а)  ; б)
; б)  ; в)
; в)  .
.
3. Запишите уравнение прямой, заданной точкой и вектором нормали.
4. Составьте уравнение прямой, проходящей через:
а) точку М(–1; 5) перпендикулярно вектору  ;
;
б) начало координат перпендикулярно вектору 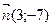 ;
;
в) точку Р(2; –4) перпендикулярно вектору  .
.
5. Что понимают под расстоянием от точки  до прямой l, если
до прямой l, если 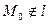 ?
?  ?
?
6. Запишите формулу нахождения расстояния от точки  до прямой l:
до прямой l: 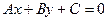 .
.
7. Найдите расстояние от точки 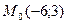 до прямой
до прямой  .
.
8. Дайте определение направленного угла между двумя прямыми.
9. Напишите формулу нахождения косинуса направленного угла между прямыми, заданными общими уравнениями.
|
|
|
10. Найдите направленный угол между прямыми  и
и  .
.
11. Напишите формулу нахождения тангенса направленного угла между прямыми, заданными уравнениями с угловым коэффициентом.
12. Найдите направленный угол между прямыми  и
и 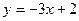 .
.
13. Каково условие перпендикулярности прямых, заданных: а) общими уравнениями; б) уравнениями с угловым коэффициентом?
14. Выясните, какие из данных прямых взаимно перпендикулярны:
а)  и
и 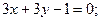 б)
б)  и
и 
в)  и
и  г)
г) 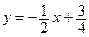 и
и 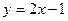 .
.
II. Типовые задачи с решениями
 Задача 1. Составьте уравнение прямой, проходящей через точку М(–3; 2) и перпендикулярной прямой d:
Задача 1. Составьте уравнение прямой, проходящей через точку М(–3; 2) и перпендикулярной прямой d: 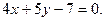
Решение. Первый способ. Уравнение искомой прямой запишем в виде  В качестве вектора нормали
В качестве вектора нормали  искомой прямой можно взять направляющий вектор
искомой прямой можно взять направляющий вектор 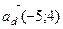 данной прямой d (рис. 25). Уравнение прямой l примет вид:
данной прямой d (рис. 25). Уравнение прямой l примет вид: 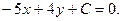 Точка М(–3: 2) лежит на этой прямой, поэтому ее координаты должны удовлетворять ее уравнению:
Точка М(–3: 2) лежит на этой прямой, поэтому ее координаты должны удовлетворять ее уравнению: 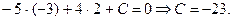
Итак, уравнение прямой l имеет вид  или
или  .
.
Второй способ. Можно воспользоваться уравнением 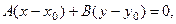 где вектор нормали прямой l
где вектор нормали прямой l 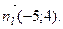
Получим: 

Ответ:  .
.
 Задача 2. Дан треугольник с вершинами P(2; –1), Q(6; –4), R(10; 3). Найдите длину высоты, опущенной из точки R.
Задача 2. Дан треугольник с вершинами P(2; –1), Q(6; –4), R(10; 3). Найдите длину высоты, опущенной из точки R.
Решение. Задача сводится к вычислению расстояния от точки R до прямой PQ (рис. 26). Уравнение прямой PQ найдем как уравнение прямой, проходящей через две точки:  Отсюда имеем:
Отсюда имеем:  или
или 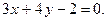
Теперь найдем расстояние d от точки R(10; 3) до этой прямой:  Следовательно, длина высоты равна 8.
Следовательно, длина высоты равна 8.
Ответ: 8.
Задача 3. Луч света, направленный по прямой 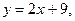 отразился от оси абсцисс. Найдите точку А пересечения луча с осью и составьте уравнение отраженного луча.
отразился от оси абсцисс. Найдите точку А пересечения луча с осью и составьте уравнение отраженного луча.
 Решение. Пусть
Решение. Пусть 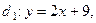
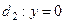 (ось абсцисс) (рис. 27). Найдем точку пересечения луча с осью Ox, т. е. точку пересечения прямых
(ось абсцисс) (рис. 27). Найдем точку пересечения луча с осью Ox, т. е. точку пересечения прямых  и
и 
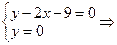
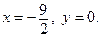 Следовательно,
Следовательно, 
Найдем тангенс направленного угла j между прямыми  и
и 

|
|
|
Тогда 
Искомую прямую d зададим уравнением  Найдем
Найдем 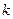 .
.


 или
или 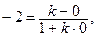 откуда
откуда 
Уравнение прямой d примет вид: 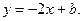 Так как
Так как  то
то  откуда
откуда 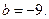
Уравнение прямой  или
или 
Ответ:  ,
, 
|
|
|


