 |
Занятие 15. Тема: «Эллипс. Гипербола. Парабола». I. Контрольные вопросы и задания. II. Типовые задачи с решениями
|
|
|
|
Занятие 15
Тема: «Эллипс. Гипербола. Парабола»
Литература для самостоятельного изучения темы: [1], гл. VI; [2], разд. I, гл. 1; [3], гл. 5; [4], гл. 5; [5], гл. III; [6], гл. III; [7], гл. 6; [8], гл. 6; [9], гл. 3; [10], гл. 3.
I. Контрольные вопросы и задания
1. Дайте определения эллипса, его фокусов, фокального расстояния, фокальных радиусов точки эллипса.
2. Запишите каноническое уравнение эллипса; дайте определения большой и малой полуосей эллипса. Какова зависимость между a, b и c?
3. Сформулируйте геометрические свойства эллипса 
Дайте определения вершин и осей эллипса.
4. Как найти координаты фокусов и вершин эллипса?
5. Дайте определение эксцентриситета эллипса. В каких пределах он находится?
6. Дайте определение директрис эллипса. Напишите уравнения директрис.
7. Дайте определение гиперболы, ее фокусов, фокального расстояния, фокальных радиусов точки гиперболы.
8. Запишите каноническое уравнение гиперболы; дайте определения действительной и мнимой полуосей гиперболы. Какова зависимость между a, b и c?
9. Сформулируйте геометрические свойства гиперболы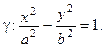 
Дайте определения вершин гиперболы, действительной и мнимой осей гиперболы.
10. Запишите уравнения асимптот гиперболы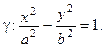
11. Дайте определение эксцентриситета гиперболы. В каких пределах он находится?
12. Дайте определение директрис гиперболы. Напишите уравнения директрис гиперболы.
13. Дайте определение гиперболы, сопряженной гиперболе 
14. Дайте определения параболы, ее фокуса, директрисы, фокального параметра.
15. Может ли быть фокальный параметр параболы нулем? отрицательным числом? Почему?
16. Запишите каноническое уравнение параболы. Сформулируйте геометрические свойства параболы.
|
|
|
17. Чему равны координаты фокуса параболы?
18. Напишите уравнение директрисы параболы.
19. Чему равен эксцентриситет параболы?
II. Типовые задачи с решениями
Задача 1. Дано уравнение гиперболы 
Найдите действительную и мнимую полуоси, фокальное расстояние, координаты вершин, фокусов, эксцентриситет, уравнения асимптот и директрис, уравнение сопряженной с ней гиперболы. Изобразите данную гиперболу и гиперболу, ей сопряженную.
Решение. Приведем уравнение гиперболы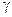 
к каноническому виду. Для этого перенесем (-144) в правую часть и разделим обе части уравнения на 144: 
Из полученного канонического уравнения находим: 
уравнения асимптот: 
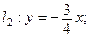уравнения директрис: 
Уравнение гиперболы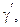 
сопряженной данной: 
 |
Строим на плоскости прямоугольную декартову систему координат
и изображаем гиперболу 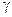, ее асимптоты, фокусы, директрисы и гиперболу 
(рис. 30).
Задача 2. Найдите каноническое уравнение эллипса, если известен его эксцентриситет 
и координаты точки 
принадлежащей эллипсу. Постройте изображение данного эллипса, его фокусов и директрис.
Решение. Каноническое уравнение эллипса имеет вид 
где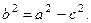 
Чтобы найти каноническое уравнение данного эллипса g, надо найти a и b.
Так как , то 
Так как 
то ее координаты удовлетворяют уравнению эллипса, т. е. 
Итак, получаем систему трех уравнений с тремя неизвестными a, b и c:
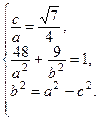
Решим эту систему. Из первого уравнения выразим c и подставим в третье уравнение: 
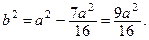Подставляем 
во второе уравнение системы: 
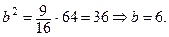
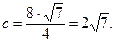
Каноническое уравнение g имеет вид: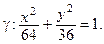 
Строим на плоскости прямоугольную декартову систему координат и эллипс g. Его фокусы имеют координаты: 
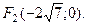
Чтобы построить директрисы, найдем их уравнения: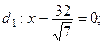 
Изображение эллипса дано на рис. 31.
 |
Задача 3. Найдите каноническое уравнение параболы и изобразите эту параболу, ее фокус и директрису, если известны координаты ее фокуса F(2; 0).
|
|
|
Решение. Так как абсцисса фокуса F положительна, то каноническое уравнение параболы имеет вид: 
.
Найдем фокальный параметр р.
Известно, что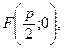 
поэтому 
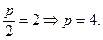Тогда каноническое уравнение параболы имеет вид: 
Уравнение директрисы 
Для построения параболы найдем координаты четырех ее вспомогательных точек, пользуясь уравнением параболы: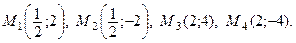 
Выбираем на плоскости прямоугольную декартову систему координат , строим точки М1, М2, М3, М4 и через эти точки и вершину параболы О проводим параболу g. Затем строим фокус F(2; 0) и директрису 
(рис. 32).
III. Задачи для упражнений
1. Дано каноническое уравнение эллипса 
Найдите большую и малую полуоси, фокальное расстояние, координаты вершин, фокусов, эксцентриситет, уравнения директрис и фокальные радиусы точки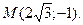 
2. Дано каноническое уравнение параболы y2 = 7x. Найдите фокальный параметр параболы, координаты фокуса и уравнение директрисы.
3. Найдите каноническое уравнение эллипса и изобразите этот эллипс, его фокусы и директрисы, если известно, что малая полуось равна 3, уравнения директрис 
и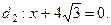 
4. Найдите каноническое уравнение гиперболы и изобразите эту гиперболу, ее асимптоты, фокусы и директрисы, если известно, что фокальное расстояние равно 
, уравнения асимптот 
мнимая ось гиперболы.
5. Найдите каноническое уравнение параболы с осью Ox и изобразите эту параболу, ее фокус и директрису, если вершина параболы находится в начале координат и парабола проходит через точку Q(1; –2).
|
|
|
