 |
II. Типовые задачи с решениями
|
|
|
|
II. Типовые задачи с решениями
Задача 1. В каждом из следующих случаев найдите уравнение плоскостиa, проходящей:
а) через точку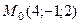 
и содержащей ось Ox;
б) через точки 
и 
параллельно оси Oy;
в) через точку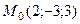 
параллельно плоскости Oxy.
Решение. а) Так как плоскость проходит через ось Ox, то точка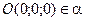 
и вектор 
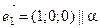. Следовательно, плоскость a задается точкой 
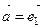и двумя неколлинеарными векторами 
и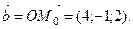 
Поэтому уравнение плоскости запишется так:
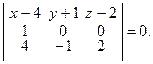После упрощений получим: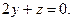 
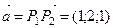б) Плоскость a задана точкой и двумя неколлинеарными векторами 
и 
Уравнение плоскости запишется так:
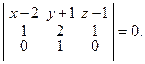После упрощения получим: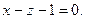 
в) Уравнение z = 0 определяет плоскость Oxy. Искомая плоскость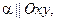 
поэтому ее уравнение будет иметь вид: 
Так как точка 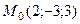принадлежит плоскости a, то ее координаты удовлетворяют данному уравнению: 
откуда D = –3. Значит, 
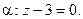
Ответ: а)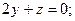 
б) 
в) 
Задача 2. Даны вершины тетраэдра A(4; 0; 2), B(0; 5; 1), C(-4; 1; 3) и D(-3; 1; 5). Напишите:
а) уравнение плоскости, проходящей через ребро АВ и параллельной ребру CD;
б) уравнение плоскости, проходящей через вершину А и параллельной грани ABCD.
Решение. а) Пусть 
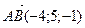– искомая плоскость. Плоскость a можно задать точкой А и двумя неколлинеарными векторами 
и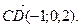 
Поэтому уравнение плоскости a запишется так:
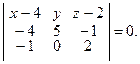После упрощений получим: 
б) Первый способ. Найдем уравнение плоскости (BCD) как плоскости, проходящей через три точки:
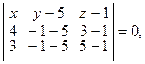откуда (ВСD):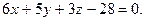 
Так как искомая плоскость a параллельна грани BCD, то ее уравнение имеет вид 
По условию задачи искомая плоскость проходит через вершину А, значит, ее координаты удовлетворяют уравнению плоскости, т. е. 
Итак,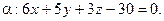 
Второй способ. Искомая плоскость a задается точкой А и двумя неколлинеарными векторами 
и 
|
|
|
откуда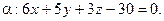
Ответ: а)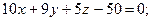 
б) 
Задача 3. Составьте уравнения плоскостей, параллельных плоскости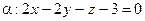 
и отстоящих от нее на расстоянии d = 5.
Решение. Пусть 
и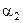 
– искомые плоскости. Так как они параллельны плоскости a, то их уравнения имеют вид: 
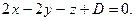Найдем координаты какой–либо точки 
, принадлежащей данной плоскости. Для этого придадим двум переменным произвольные значения, например, 
, 
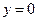и найдем значение третьей переменной: 
Точка 
принадлежит данной плоскости a. 
т. е. 
откуда 
или 
или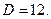 
Значит,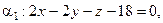 
Ответ: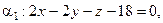
Задача 4. Найдите высоту пирамиды HD, вершины которой находятся в точках 
B(1; 0; –4), C(–1; 3; 0), D(0; 3; –5).
Решение. Высоту пирамиды можно найти как расстояние от точки D до плоскости (АВС). Составим уравнение плоскости (АВС) как уравнение плоскости, проходящей через три точки: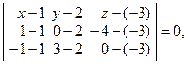 
откуда 
После упрощений получим: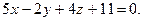 
Теперь найдем расстояние от точки D до плоскости (АВС):
Итак, 
Ответ:
III. Задачи для упражнений
1. Даны уравнения трех граней параллелепипеда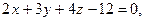 
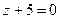и одна из вершин (6; –5; 1). Найдите уравнения трех других граней.
2. Через линию пересечения плоскостей 
и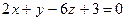 
проведите плоскость, проходящую через середину отрезка АВ, если АВ(1; 4; 0) и В(5; 2; –4).
3. Составьте уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям: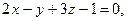 
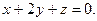
4. Две грани куба лежат на плоскостях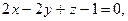 
Вычислите объем этого куба.
5. Найдите величину угла между гранями ACD и ABD тетраэдра ABCD, если A(3; 0; –1), B(2; 1; 1), C(3; 1; 0), D(4; 0; 0).
6. На оси Oy найдите точку, отстоящую от плоскости 
на расстоянии 
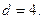
IV. Задачи для самостоятельного решения
1. При каком значении свободного члена D плоскость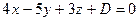 
пересекает ось: а) Ox; б) Oy; в)Oz?
2. На оси Oz найдите точку А, равноудаленную от начала координат и от плоскости 
3. Установите, что три плоскости 
имеют одну общую точку и вычислите ее координаты.
|
|
|
4. Определите, при каких значениях а и b плоскости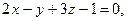 
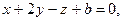
1) имеют одну общую точку; 2) проходят через одну прямую; 3) пересекаются по трем различным параллельным прямым.
5. Составьте уравнение плоскости, проходящей через ось Oz перпендикулярно к плоскости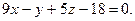 
6. Составьте уравнение плоскости проходящей через точки А(1; 0; –1), В(1; 3; –4) и образующей угол 
с плоскостью 
|
|
|
