 |
II. Типовые задачи с решениями
|
|
|
|
II. Типовые задачи с решениями
Задача 1. Составьте уравнение прямой, проходящей через точку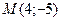 
и параллельной прямой 
Решение. Первый способ. Искомое уравнение имеет вид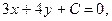 
где С пока не определено. Вид уравнения следует из условия параллельности двух прямых 
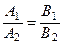или 
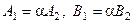при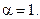 
Чтобы найти значение С, необходимо подставить координаты точки М в искомое уравнение. Точка М лежит на прямой, поэтому ее координаты должны удовлетворять уравнению этой прямой. Подставляя координаты 
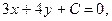в уравнение получаем: 
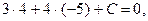откуда 
Таким образом, уравнение прямой имеет вид: 
Второй способ. Из параллельности искомой и данной прямой следует, что направляющий вектор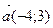 
данной прямой будет и направляющим вектором искомой прямой. Запишем каноническое уравнение искомой прямой: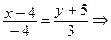 
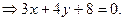
Третий способ. Запишем уравнение данной прямой с угловым коэффициентом: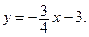 
Искомая прямая проходит через точку М, следовательно, можно записать уравнение прямой, проходящей через данную точку, с данным угловым коэффициентом: 
т. е.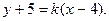 
Так как искомая прямая параллельна данной прямой, то их угловые коэффициенты совпадают. Тогда уравнение прямой примет вид: 
или Ответ:
Задача 2. Даны уравнения двух сторон прямоугольника 
и одна из его вершин 
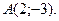Составьте уравнения двух других сторон этого прямоугольника.
Решение. Выясним, какие даны стороны прямоугольника, смежные или противоположные. Так как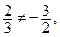 
то данные стороны не параллельны, значит, они смежные. Точка А не принадлежит данным сторонам, так как ее координаты не удовлетворяют уравнениям сторон (проверьте). Найдем уравнение прямой, проходящей через точку А и параллельной прямой 
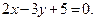Искомое уравнение имеет вид 
Подставим координаты точки А в искомое уравнение, получим 
откуда С = –13. Значит, одна из искомых сторон прямоугольника имеет уравнение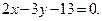 
Аналогично находим уравнение стороны, параллельной прямой . Оно имеет вид 
.
|
|
|
Ответ: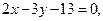 
.
Задача 3. Даны середины сторон треугольника: 
и 
Составьте уравнения его сторон.
Решение. Так как 
то вектор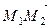 
можно принять за направляющий вектор прямой АВ (рис. 24). Его координаты найдем через координаты точек М1 и М2: 
Итак, прямая АВ задана точкой М3(3; –4) и направляющим вектором
Воспользуемся каноническим уравнением прямой: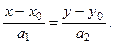 
В нашем случае 
отсюда 
Аналогично можно найти уравнения прямых АС и ВС.
III. Задачи для упражнений
1. Составьте уравнение прямой, проходящей через точку М(7; -2)
а) параллельно оси Ox;
б) параллельно оси Oy;
в) параллельно биссектрисе координатных углов;
г) параллельно прямой y = 5x + 3.
2. Составьте уравнения медиан треугольника, вершины которого находятся в точках А(2; 3), В(–3; 5) и С(7; –1).
3. Даны уравнения двух сторон параллелограмма 8x + 3y + 1 = 0, 2x + y – 1 = 0 и уравнение одной из диагоналей 3x + 2y + 3 = 0. Определите координаты вершин этого параллелограмма.
4. Покажите, что четырехугольник ABCD, где A(–2; –2), B(–3; 1), C(7; 7) и D(3; 1), является трапецией. Составьте уравнения средней линии и диагоналей этой трапеции.
5. При коком значении а следующие пары прямых параллельны:
а) 
и 
б) 
и 
6. Определите, при каких значениях m и n две прямые 
и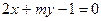 
а) параллельны; б) совпадают; в) перпендикулярны.
7. Определите, пересекаются ли в одной точке три прямые: 
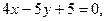
IV. Задачи для самостоятельного решения
1. Стороны треугольника расположены на прямых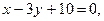 
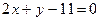и 
Через вершины этого треугольника проведите прямые, параллельные противолежащим сторонам.
2. Даны координаты трех вершин параллелограмма ABCD: A(–1; 2), B(–2; –2), C(5; –2). Составьте уравнения его диагоналей АС и BD.
|
|
|
3. Составьте уравнения сторон треугольника АВС, если даны одна из его вершин А(1; 3) и уравнения двух медиан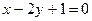 
и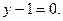 
4. Определите, при каком значении а три прямые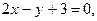 
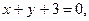
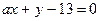будут пересекаться в одной точке.
|
|
|
