 |
IV. Задачи для самостоятельного решения
|
|
|
|
IV. Задачи для самостоятельного решения
1. Определите эксцентриситет эллипса, зная, что расстояние между его директрисами в 4 раза больше расстояния между фокусами.
2. Найдите каноническое уравнение гиперболы, имеющей общие фокусы с равносторонней гиперболой 
и проходящей через точку (5; 3). Постройте изображение гиперболы.
3. На первой ветви гиперболы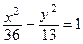 
найдите точки, фокальный радиус которых равен 8.
4. Составьте каноническое уравнение гиперболы, имеющей общие фокусы с эллипсом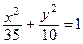 
и проходящей через точку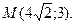 
5. Меридиан земного шара имеет форму эллипса, отношение осей которого равно 
Определите эксцентриситет земного меридиана.
6. Стальной трос подвешен за два конца. Точки крепления расположены на одинаковой высоте. Расстояние между ними равно 20 м. Величина его прогиба на расстоянии 2 м от точки крепления, считая по горизонтали, равна 14, 4 см. Определите величину прогиба этого троса в середине между точками крепления, приближенно считая, что трос имеет форму дуги параболы.
7. Поперечное сечение крыши вагона имеет форму параболы. Ширина крыши 3, 6 м. Определите высоту крыши, если на расстоянии 1, 44 м от края высота крыши 0, 48 м.
8. Камень, брошенный под острым углом к горизонту, описал дугу параболы и упал на расстоянии в 16 м от начального положения. Определите параметр параболической траектории, зная, что наибольшая высота, достигаемая камнем, равна 12 м.
9. Составьте каноническое уравнение параболы, зная, что парабола симметрична относительно оси Oy и проходит через начало координат, а прямая y – 2 = 0 пересекает параболу в точках с абсциссами 3 и (–3).
V. Задание на дом
1. Найдите каноническое уравнение эллипса, если расстояние между фокусами равно 6, а большая полуось равна 5. Изобразите этот эллипс.
|
|
|
2. Найдите каноническое уравнение эллипса, если его малая полуось равна 4, эксцентриситет равен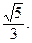 
Изобразите этот эллипс.
3. Найдите каноническое уравнение гиперболы с мнимой осью Oy, если мнимая полуось равна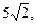 
уравнения директрис 
Изобразите эту гиперболу.
4. Найдите каноническое уравнение гиперболы с мнимой осью Oy, если гипербола проходит через точку 
уравнения асимптот 
Изобразите эту гиперболу.
5. Найдите каноническое уравнение параболы, вершина которой находится в начале координат, и изобразите эту параболу, если уравнение директрисы 
Занятие 16
Тема: «Изучение поверхностей второго порядка
по их каноническим уравнениям»
Литература для самостоятельного изучения темы: [1], гл. XVIII; [2], разд. I, гл. 3; [3], гл. 5; [4], гл. 5; [5], гл. III; [6], гл. IV; [7], гл. 6; [8], гл. 6; [9], гл. 9; [10], гл. 10.
I. Контрольные вопросы и задания
1. Дайте определения эллипсоида, канонического уравнения эллипсоида, полуосей эллипсоида.
2. Какие оси симметрии и плоскости симметрии имеет эллипсоид? Имеет ли эллипсоид центр симметрии?
3. Дайте определение вершин эллипсоида. Сколько вершин имеет эллипсоид?
4. Что представляет собой сечение эллипсоида координатной плоскостью Oxy? Oxz? Oyz?
5. Какой эллипсоид называется эллипсоидом вращения? Какой вид имеет его каноническое уравнение?
6. Как получить каноническое уравнение сферы из канонического уравнения эллипсоида?
7. Дайте определения однополостного и двуполостного гиперболоидов, их канонических уравнений и полуосей.
8. Какие оси симметрии и плоскости симметрии имеют однополостный и двуполостный гиперболоиды? Имеют ли эти поверхности центр симметрии?
9. Дайте определение вершин однополостного (двуполостного) гиперболоида. Сколько вершин имеют однополостный и двуполостный гиперболоиды?
|
|
|
10. Что представляет собой сечение однополостного (двуполостного) гиперболоида координатной плоскостью Oxy? Oxz? Oyz?
11. Дайте определения однополостного и двуполостного гиперболоидов вращения. Каковы их канонические уравнения?
12. Дайте определения эллиптического и гиперболического параболоидов, их канонических уравнений.
13. Какие оси симметрии и плоскости симметрии имеют эллиптический и гиперболический параболоиды?
14. Дайте определение вершины параболоида.
15. Что представляет собой сечение эллиптического (гиперболического) параболоида координатной плоскостью Oxy? Oxz? Oyz?
16. Дайте определение эллиптического параболоида вращения. Какое каноническое уравнение он имеет?
17. Дайте определения цилиндрической поверхности и цилиндрической поверхности второго порядка.
18. Дайте определения направляющей линии цилиндрической поверхности и образующих цилиндрической поверхности.
19. Напишите каноническое уравнение: а) эллиптического цилиндра; б) гиперболического цилиндра; в) параболического цилиндра.
20. Дайте определения конуса второго порядка, канонического уравнения конуса, вершины конуса.
21. Какие оси симметрии и какие плоскости симметрии имеет конус второго порядка?
22. Запишите каноническое уравнение конуса вращения.
|
|
|
