 |
III. Задачи для упражнений. IV. Задачи для самостоятельного решения. V. Задание на дом. Занятие 12. Тема: «Плоскость в пространстве»
|
|
|
|
III. Задачи для упражнений
1. Точка А(2; –5) является вершиной квадрата, одна из сторон которого лежит на прямой 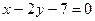 . Вычислите площадь этого квадрата.
. Вычислите площадь этого квадрата.
2. Вычислите расстояние между параллельными прямыми:
а)  и
и  б)
б) 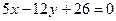 и
и  .
.
3. Определите координаты точки, симметричной точке М(–1; 3) относительно прямой 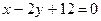 .
.
4. Даны вершины треугольника 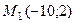 и
и  ; его высоты пересекаются в точке N(5; 2). Определите координаты третьей вершины
; его высоты пересекаются в точке N(5; 2). Определите координаты третьей вершины 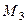 .
.
5. Луч света направлен по прямой  . Дойдя до прямой
. Дойдя до прямой 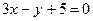 , он отразился. Составьте уравнение прямой, на которой лежит отраженный луч.
, он отразился. Составьте уравнение прямой, на которой лежит отраженный луч.
6. Составьте уравнение прямой, проходящей через точку Р(–2; 3) на одинаковых расстояниях от А(5; –1) и В(3; 7).
7. Составьте уравнения биссектрис углов, образованных прямыми 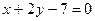 и
и  .
.
IV. Задачи для самостоятельного решения
1. Даны вершины треугольника А(–10; –13), В(–2; 3) и С(2; 1). Вычислите длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С.
2. Даны две вершины А(3; –1) и В(5; 7) треугольника АВС и точка N(4; –1) пересечения его высот. Составьте уравнения сторон этого треугольника.
3. Составьте уравнения сторон треугольника, зная одну из его вершин А(4; –1) и уравнения двух биссектрис 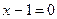 и
и  .
.
4. Диагональ квадрата расположена на прямой 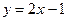 . Одна из его вершин находится в точке А(4; –3). Составьте уравнения его сторон и второй диагонали.
. Одна из его вершин находится в точке А(4; –3). Составьте уравнения его сторон и второй диагонали.
5. Составьте уравнение биссектрисы угла между прямыми  и
и  , смежного с углом, содержащим начало координат.
, смежного с углом, содержащим начало координат.
V. Задание на дом
1. Даны уравнения двух сторон прямоугольника  ,
, 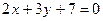 и одна из его вершин А(–2; 1). Вычислите площадь этого прямоугольника.
и одна из его вершин А(–2; 1). Вычислите площадь этого прямоугольника.
2. При каком значении b следующие пары прямых перпендикулярны:
а)  и
и  б)
б) 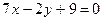 и
и 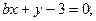
|
|
|
в) 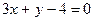 и
и  ?
?
3. Две прямые пересекаются в точке А(2; –1). Одна из них проходит через начало координат, другая – через точку В(5; 1). Найдите направленный угол между этими прямыми.
4. Составьте уравнения катетов равнобедренного прямоугольного треугольника, если уравнение гипотенузы  и вершина прямого угла С(3; 4).
и вершина прямого угла С(3; 4).
5. На оси ординат найдите точку А, находящуюся на одинаковом расстоянии от начала координат и от прямой  .
.
Занятие 12
Тема: «Плоскость в пространстве»
Литература для самостоятельного изучения темы: [1], гл. X; [2], разд. I, гл. 2; [3], гл. 4; [4], гл. 4; [5], гл. II; [6], гл. II; [7], гл. 5; [8], гл. 5; [9], гл. 9; [10], гл. 10.
I. Контрольные вопросы и задания
1. Напишите следующие уравнения плоскости:
а) векторное; б) параметрические;
в) уравнение плоскости, заданной точкой и двумя неколлинеарными векторами;
г) уравнение плоскости, проходящей через три точки.
2. Выясните, принадлежит ли точка М(–1; –2; 3) плоскости, заданной уравнением:
а) 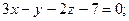 б)
б) 
3. Определите координаты нескольких точек, лежащих в плоскости  .
.
4. Каковы частные случаи общего уравнения плоскости? Изобразите плоскость, уравнение которой:
а) 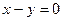 ; б)
; б)  ; в)
; в) 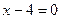 ; г)
; г) 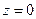 ; д)
; д) 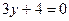 .
.
5. Запишите условие параллельности вектора  плоскости
плоскости 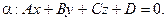 Какие из векторов
Какие из векторов 


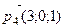 параллельны плоскости
параллельны плоскости  ?
?
6. Составьте уравнение плоскости, проходящей через точку М(1; –3; 2) параллельно векторам 
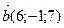 .
.
7. Составьте уравнение плоскости, проходящей через три точки 
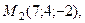

8. Дайте определение вектора нормали плоскости. Найдите координаты вектора нормали плоскости, заданной в прямоугольной декартовой системе координат:
а) 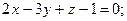 б)
б) 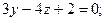 в)
в) 
9. Запишите уравнение плоскости, заданной точкой  и вектором нормали
и вектором нормали  Найдите общее уравнение плоскости
Найдите общее уравнение плоскости  , заданной точкой
, заданной точкой 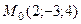 и вектором нормали
и вектором нормали 
10. Напишите формулу нахождения расстояния от точки  до плоскости
до плоскости 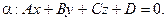 Найдите расстояние от точки
Найдите расстояние от точки 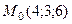 до плоскости
до плоскости 
|
|
|
11. Напишите формулу нахождения угла между плоскостями. Найдите угол между плоскостями 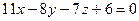 и
и 
12. Запишите условия параллельности и перпендикулярности двух плоскостей  и
и 
13. Установите взаимное расположение следующих пар плоскостей:
а) 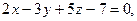
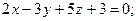
б) 

в) 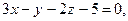
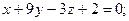
г) 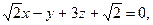

д) 
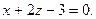
14. Найдите расстояние между параллельными плоскостями: 
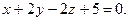
|
|
|


