 |
V. Задание на дом. Занятие 13. Тема: «Прямая в пространстве». I. Контрольные вопросы и задания. II. Типовые задачи с решениями
|
|
|
|
V. Задание на дом
1. Составьте уравнение плоскости, которая проходит:
а) через точку М(1; –2; 4) параллельно плоскости Oxz;
б) через точку Q(3; –4; 7) и ось Oz;
в) через точки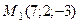 
и 
параллельно оси Ox.
2. Найдите расстояние точки (4; 3; 0) от плоскости, проходящей через точк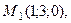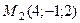и 
и 
3. Напишите уравнение плоскости, проходящей через начало координат перпендикулярно плоскостям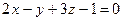 
и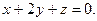 
4. Напишите уравнения плоскостей, параллельных плоскости 
и отстоящих от нее на расстоянии d = 5.
Занятие 13
Тема: «Прямая в пространстве»
Литература для самостоятельного изучения темы: [1], гл. X; [2], разд. I, гл. 3; [3], гл. 4; [4], гл. 4; [5], гл. II; [6], гл. II; [7], гл. 5; [8], гл. 5; [9], гл. 9; [10], гл. 10.
I. Контрольные вопросы и задания
1. Запишите канонические уравнения прямой и объясните смысл буквенных обозначений.
2. Напишите канонические уравнения прямой, проходящей через точку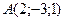 
параллельно вектору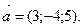 
3. Как можно получить из канонических уравнений прямой ее параметрические уравнения?
4. Запишите общие уравнения прямой. Какому условию должны удовлетворять коэффициенты, чтобы уравнения совместно определяли прямую?
5. Определите координаты нескольких точек, лежащих на прямых:
а)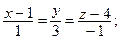 
б) 
в) 
6. Как можно перейти от общих уравнений прямой к ее каноническим уравнениям?
7. При каких условиях две прямые, заданные в пространстве:
а) скрещиваются; б) пересекаются; в) параллельны; г) совпадают?
8. Дайте определение угла между двумя прямыми в пространстве.
9. Напишите формулу нахождения косинуса угла между прямыми. Определите угол между прямым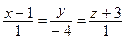и 
и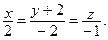 
10. Напишите условие перпендикулярности двух прямых в пространстве.
|
|
|
II. Типовые задачи с решениями
Задача 1. Найдите канонические уравнения прямой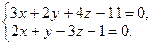 
Решение. Полагая, например, 
из системы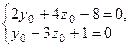 
получаем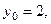 
Таким образом, точка 
прямой найдена.
Теперь определим направляющий вектор 
данной прямой: 
т. е. 
Запишем канонические уравнения прямой: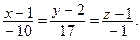 
Ответ: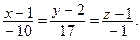
Задача 2. Докажите, что прямые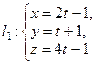 
и 
пересекаются. Найдите точку их пересечения
Решение. Прямая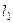 
задана фиксированной точкой 
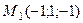и направляющим вектором 
. Прямая 
задана фиксированной точкой 
и направляющим вектором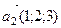 
.
Докажем, что прямые 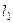и лежат в одной плоскости, т. е. что смешанное произведение векторов 
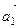и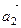 
равно нулю, и что векторы 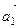и 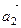не коллинеарны.
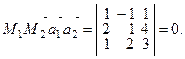
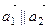, т. к. 
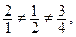значит, прямые 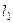и пересекаются.
Составим из их канонических уравнений систему:
Решив ее, находим координаты точки пересечения данных прямых:
x = 1, y = 2, z = 3.
Ответ: (1; 2; 3).
III. Задачи для упражнений
1. Составьте уравнение прямой:
а) проходящей через две точки 
;
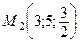б) проходящей через точку 
параллельно вектору 
;
в) образованной пересечением плоскости 
с координатной плоскостью Oxy.
2. Напишите параметрические уравнения следующих прямых:
а) 
б) 
3. Через точку М(1; –3; 4) проведите прямую, параллельную прямой 
4. Найдите тупой угол между прямыми: 
и 
5. Установите взаимное расположение следующих пар прямых:
а)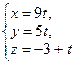 
и 
б) 
и 
в) 
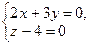и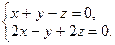 
6. Составьте уравнение плоскости, проходящей через прямую 
и параллельной прямой 
IV. Задачи для самостоятельного решения
1. Составьте уравнение прямой, которая проходит через точку 
и пересекает прямые 
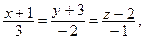
2. Через точку А(1; 0; –1) проведите прямую, перпендикулярную к прямой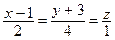 
и пересекающую прямую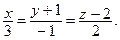 
3. При каком D прямая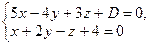 
пересекает ось Oy?
4. Найдите расстояние точки М(2; –1; 3) от прямой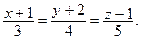 
V. Задание на дом
1. Найдите острый угол между прямыми: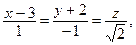 
2. Докажите перпендикулярность прямых: 
и 
|
|
|
3. Докажите параллельность прямых: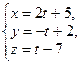 
и 
4. Установите взаимное расположение прямых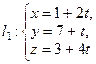 
и 
5. Определите координаты точки, лежащей на прямой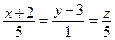 
и имеющей ординату, равную –1.
|
|
|
