Албанская философская и общественная мысль—алгебра логики 33 1 глава

воспевали любовь, жизнь, радость, печаль и обяза­тельно — бога. К той же школе примыкал писатель Хасан Зюко Камбери.

Дальнейшее разлитие фил ос. и обществ, мысли в Албании приходится на 19 в., когда стал распростра­няться бекташизм, враждебный офиц. идеологии суннизма. Идеологами бекташизма, писавшими на алб. языке, были Д. Фрашери, Ш. Фрашери и др. Бекта-шисты стояли на пантеистич. позициях, требовали упрощения церк. церемоний и т. д.

Новый этап в развитии обществ.мысли Албаниипри-ходится на 2-ю пол. 19 в.— период, известный под назв. «Национального албанского Возрождения». В области социально-экономической он характеризует­ся распадом феод, отношений и зарождением элемен­тов капитализма, в социально-политической — раз­витием нац.-освободит, борьбы и нац. самосознания. Руководители нац. движения являлись в то же время выдающимися мыслителями. Воспитанные в основном на вост. художеств, лит-ре и философии, они связывали свои филос. взгляды с борьбой за упрочение нац. само­сознания, за единение алб. народа. Начиная с II. Ве-кильхарджи (1797 —1867), деятели Возрождения при­зывали своих соотечественников, принадлежавших к разным вероисповеданиям, ставить пац. единство выше религиозного. Не отказываясь от веры в силу божества, деятели Возрождения критиковали церк. институты, указывая, что они служат интересам поли­тики иностранцев: мусульм. храмы —тур. политике, православные — эллинизаторской политике, а католи­ческие—экспансионистской политике Австро-Венгрии.

Филос. идеи содержатся в трудах Н. Фрашери (1846—1900), выдающегося алб. поэта периода Нац. Возрождения. Противник тур. ига, он был также вра­гом мусульм. религ. догматики. Борьбу с религ. идеологией Фрашери вел с позиций пантеизма. Соглас­но Фрашери, бог не сверхъестеств., потустороннее существо, а начало естественное, имманентное при­роде. Рассматривая бога в качестве сущности вещей, Фрашери растворял бога в обожествляемой им мате­рии. Пантеизм Фрашери сочетался с естеств.-науч. представлениями о миро, происхождении Земли и эволюции человека. Вселенная для него не только бесконечна в пространстве, но и вечна во времени. Фрашери выдвигал идею о диалсктич. развитии мира, однако он но был последователен в этом вопросе. Его пантеизм являлся переходной ступенью к материализ­му. С одной стороны, он признавал, что мир находится в вечном непрерывном движении, с другой стороны — утверждал, что это развитие совершается по кругу, как простое повторение.

Филос. и социально-политич. мысль в Албании в дальнейшем развивалась в работах идеолога нац. алб. движевия С. Фрашери (1850—1903). Он требовал пол­ного отделения Албании от Турецкой империи, был сто­ронником респ. правления. В области философии С. Фрашери стоял на позициях объективного идеализ­ма, признавал существование бога как творца Вселен­ной. Вместе с тем он придавал большое значение разу­му, науке как орудиям цивилизации.

В первом десятилетии 20 в. в Албанию проникают идеи социализма. После провозглашения независимо­сти Албании (1912) страна неск. лет находилась под иностр. оккупацией. На разрешение внутр. проблем гос. устройства Албании оказала влияние Окт. револю­ция в России. 1920—24 гг. характеризовались мощ­ным подъемом демократич. движения в Албании, подго­товившего бурж.-демократич. революцию (июнь 1924).

В окт. 1924 контрреволюционеры во главе с А. Зогу с помощью иностр. империалистов установили реакц. режим, к-рый существовал вплоть до 1939, когда Алба­ния была захвачена фашистской Италией. Годы режима •iory характеризовались обострением классовой борь-

бы и подготовкой условий для создания нац. антифа­шистского фронта. В этот период в Албании распро­странялись идеи марксизма и в условиях подполья в гл. пром. центрах страны возникали первые комму-нистич.организации.Обострениевнутриполитич. поло­жения отражалось и на идеологич. борьбе. Образова­лись два лагеря. Один из них — т. н. «старики», сто­ронники господств, клики, стремившиеся в то же время сохранить старые формы тур.-вост. правления. В своем органе «Besa» они защищали монархич. режим, патриархальные формы обществ, уклада, считая их наиболее подходящими для «сохранения национальной индивидуальности», пропагандировали религ. миро­воззрение. Другой лагерь составляли идеологи новой алб. буржуазии, воспевавшие демократич. бурж. мо­нархию, сторонники нек-рых политич. и социальных реформ. Их печатный орган — журн. «Perpjekja Shqiptare» (1936—39) — боролся с материалистич. фи­лософией, пропагандировал философию О. Конта, Бергсона, Фрейда и др.

Марксистская идеология в 30-е гг. развивалась на страницах журн. «Rilindja», «Flaka», «А.В.С.». В жур­нале «Bota e Re» печатались статьи, распростра­нявшие материализм, осуждавшие фашизм, войну, капиталистич. строй и косвенным путем — режим Зогу. Подъем общественной революционной мысли в Албании наступает после основания Албанской ком-мунистич. партии (1941), ныне — Албанская партия труда (АПТ). С самого начала существования АНТ положила в основу своей деятельности теорию марксизма-ленинизма. В условиях подполья и поли­цейского террора под руководством партии был предпринят перевод многих произведений классиков марксизма-ленинизма.

Народная революция, к-рая окончилась 29 ноября 1944 освобождением страны от нем. оккупантов и уста­новлением нар. демократии, означала также и триумф марксистской идеологии в Албании. В Албании ши] око изучается марксистско-ленинская философия. В Ти-ранском ун-те и Высшей парт, школе созданы кафедры марксизма-ленинизма, ведется преподавание диалск­тич. и историч. материализма. На секциях философии этих кафедр изучается история обществ, мысли в Ал­бании, разрабатываютеявопросыдиалектич. иисторич. материализма. Органами филос. и обществ.-политич. мысли совр. Албании являются журн. «Pruga e Раг-tise» («Путь партии»), «Buletini i Universitetit Shteb-ror te Tiranes, Seria shkencat shoqrore» («Бюллетень Тиранск. ун-та. Сер. социальных наук»). Переводятся произведения классиков марксизма-ленинизма. В наст. время предпринимается издание полного собр. соч. В. И. Ленина.

Лит.: Historia e Shqiperise, v. 1. Tirane, 1959; Historia e
letersise shqipe, v. 1—2, Tirane, 1959—60; S u ff1 а у M.,Die
Kirchenzustande im Vorti.rkischen Albanien; Die Orthodoxe
Durchbrucbzone im katholischen Damme, в кн.: Illyriscii-Al-
banische Forschungen, Bd 1, M nch.— Lpz., 1916; Pall F.,
Marino Barlezio,uno storico umanista,Bnc.,1938;R uftiniM.,
Teodor Anastasie Cavallioti, scrittore Moscopolitano del secolo
XVIII, «Riv. Albania», 1942, fasc. 2; Myderrizi O., Hasan
Zyko Kamberi, «Bui. shkenc. shoqer.», 1955, №1; Spasse S.,
Mihail Grameno, там же. 1956, N° 1; X h о 1 i Z., Nairn Frashe-
ri mendimtar i shquar shqiptar, там же, 1959, № 2; H о х-
h а Е., Influence e Revolucionit te Madh te Tetorit пё Shqiperi,
Tirane, 1957. К. Фрашери. Албания.

АЛГЕБРА Л ОГИКИ — одна из осн. частей мате-матич. логики, основанная на применении алгебраич. методов к логике. Возникнув в сер. 19 в. в трудах Буля и развиваясь затем в работах Джевонса, Шредера, Пирса, Порецкого и др., А. л. имела своим предме­том классы (как объемы понятий), соотношения меж­ду ними по объему и связанные с этим операции над ними. Само создание А. л. представляло собой попытку решать традиц. логич. задачи алгебраич. (т. е. характерными для алгебры) методами. В свя­зи с появлением в 70-х гг. 19 в. теории мно-.

34 АЛГЕБРА ЛОГИКИ

жеств (см. Множеств теория), поглотившей часть прежнего предмета А. л. (теоретико-множеств. опера­ции), и дальнейшим развитием математич. логики в трудах Фреге, Рассела, Гильберта и др. (последняя четверть 19 в. и 1-я пол. 20 в.; для развития А. л. большое значение имели труды И. И. Жегалкина) предмет А. л. значительно изменился. Основным ее предметом, особенно в работах сов. ученых, яв­ляются высказывания (объекты, родств. предложе­ниям, суждения и т. п.), рассматриваемые со стороны их логич. значений (истина, ложь, бес­смыслица и т. п.), и те логич. операции над ними, для изучения к-рых достаточно иметь дело лишь с этой стороной высказываний.

Наличие у А. л. этого предмета, изучаемого не только алгебраич. методами, а также связь самих алгебраич. методов с иными математич. методами поро­ждают многочисл. связи А. л. с другими разделами ма­тематич. логики (исчисления высказываний, исчисле­ния классов, исчисления предикатов, теория функций алгебры логики, логико-математич. теория релейно-контактных схем и др.). Этим же обусловливается и нек-рое проникновение в А. л. таких методов, как ак-сиоматич. метод, методы теории алгоритмов, теории множеств (см. Теоретико-множественная логика), то­пологии и др.

Роль спец. методов в логике (в частности, матема­тич. методов, без к-рых нет и не может быть матема­тич. логики), как и в др. науках, состоит в том, что они позволяют найти новые способы подхода к изучае­мому предмету, выявить новые стороны его, важность к-рых подтверждается практикой. Так, в частности, А. л., использующая в своей основе далеко идущие абстракции, огрубление и формализацию, находит все более широкое применение в технике (осо­бенно при решении задач, связанных с построени­ем автоматов) и, наоборот, развивается сама под вли­янием запросов техники (задач автоматизации про­граммирования, уменьшения числа элементов в устройствах релейного действия и др.).

В основе обычной, т. н. классич. А. л. лежит абстракция высказывания как величины, имеющей одно (и только одно!) из двух значений: «истина» или «ложь» (короче: И, Л), или могущей принимать оба эти значения (но не одновременно). В первом из этих случаев имеем индивидуальное высказывание (высказывание в узком, наиболее принятом смысле этого слова), во втором — высказывание-функцию. Примеры выска­зываний: «2-2-4», «0 £ 0», «Сократ — человек», «0 = 1», «2-2 = = 5", «х° = У», «z — человек», «Если х = у, то у=0», «Если х=2, то х²- 4», «х равняется у или х не равняется у». Первые три высказывания имеют значение И (т. е. истинны), 4-е и 5-е— значение Л (т. е. ложны), 6-е, 7-е, 8-е — высказывания-функции (если, напр., значениями буквенных переменных х и у могут быть целые числа, а переменной z — живые су­щества), 9-е и 10-е имеют значение И (при всех возможных значениях переменных х и у). Последние три из этих выска­зываний являются сложными, в отличие от предшествующих им простых. При этом высказывание наз. сложным, если в нем есть хотя бы одна из связок «и», «или», «если..., то», «эквивалентно» и т. п. или частица «не».

Абстракция в А. л. идет дальше рассмотрения значений высказываний. Именно, все истинные высказывания отожде­ствляются между собой, т. к. истинное высказывание не от­личается от другого истинного высказывания по значению (от других сторон высказываний в А. л. отвлекаются). Ложные высказывания между собой тоже отождествляются. При рас­смотрении же высказываний-функций в А. л. обычно отвле­каются от рассмотрения зависимости их от иных перемен­ных, кроме таких, значениями к-рых являются тоже выска­зывания, вводя для их рассмотрения буквенные перемен­ные, к-рые мы будем называть переменными высказыва­ниями (точнее, переменными для высказываний). Таковыми являются буквы А,В, С,..., А,, Д„ А₃,...ит. п. (необязательно именно заглавные латинские; выбор последних — вопрос не существа А. л., а соглашения) при условии, что они играют роль переменных, значениями к-рых могут быть всевозможные индивидуальные высказывания, т. е., в силу упомянутых абстракций, «константы» И и Л. Буквенные обозначения вы­сказываний вообще характерны для А. л. подобно тому, как для обычной школьной алгебры характерны буквенные обозначения чисел. Так, не только переменные высказывания, но и индивидуальные часто обозначаются буквами А, В, С и т. п. (но играющими при этом роль констант).

Кроме простых высказываний, обозначаемых отд. буквами
А, в... или И, Л, рассматриваются также сложные высказы­
вания — результат соединения высказываний связками или
отрицания их (соответствующего частице «не»). Сложные
высказывания рассматривают как функции от входящих в них
буквенных переменных А, В,Сит. д. Так появляется понятие
функции А. л.—функции от аргументов, являющихся пере­
менными высказываниями, т. е. принимающих значения И, Л,
к-рая (функция) может принимать тоже лишь эти значения.
Для сложных высказываний в связи с этим часто употребля­
ются функциональные обозначения /(A), D (В), Ф (А, В, С),
Ф (А„ А_,... А_п) и т. п.

Однако более еистематич. употребление находят в А. л. другие обозначения — обозначения алгебраич. операций над высказываниями. Эти операции, играющие в А. л. роль, ана­логичную той, к-рую в обычной школьной алгебре играют операции сложения, вычитания, умножения и др. операции над числами, соответствуют в А. л. упомянутым выше связкам и частице «не». Так вводятся операции: конъюнкция А-В (читается «А и В»; другие обозначения: АВ, А&.В, А/\В; другие названия: логическое умножение, булево умножение), дизъюнкция А\/В (чит. «А или В»; другие обозначения: А+В, АВ;другие названия: логическое сложение, булево сложение), импликация А->В (чит.: «Если А, то В» или «А влечет В», или «А имплицирует В», или «Из А следует В»; другие обозна­чения: AZDB; другое название: логическое следование), эк-вивалепция А~В (чит.: «А эквивалентно В» или «А равнознач­но В», или «А, если и только если В»: другие обозначения: А = В,А* —>В, А^В, А=В; другие названия: эквивалент­ность, равнозначность, равносильность), отрицание А (чит.: «не А», или «А ложно», или «не верно, что А», или «отрицание А»; другие обозначения:->-А, —А, А'; другое название: ин­версия), а также иногда и др. операции.

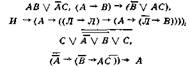
и т. п., а также, вместе с ними, такие, казалось бы, противо­естественные конструкции, как высказывания «Если 2-2=5, то все люди верблюды», «Если 0 = 1, то: если 0 = 1, то 1 = 1 и КЗ» и т. п. Нек-рые из получающихся выражений, как, напр.,

Одной из важных сторон формализации, принимаемой в А. л., является то, что знаками этих операций (т. е. по смыс­лу, соответствующими им связками) можно соединять любые высказывания, без ограничения, в т. ч. и те, к-рые сами яв­ляются сложными. Так возникают такие выражения (симво-лич. высказывания), как

даже трудно словесно высказать и приходится читать путем перечисления всех знаков, включая скобки. Зато при этом удается точно и строго описать класс всех рассматриваемых выражений А. л. В данном случае он состоит из констант И и Л, переменных А, В... и всех тех выражений, к-рые получаются из них путем конечного числа соединений знаками «■», «V», «-»» и «~» и отрицаний. В др. случаях рассматри­ваются др. классы выражений, содержащие др. знаки операций или же только эти, но не все из них.

Такие же неудобочитаемые выражения, как вышеприведен­ное, вовсе не являются «мертвым грузом» в А. л. Они могут наряду с др. выражениями получаться, напр., при анализе релейно-контактных схем или в результате преобразований других, более удобочитаемых, но громоздких выражений, что применяется, напр., при синтезе контактных схем. Да и не­обычность приведенных выше «противоестественных» выска­зываний можно усмотреть, лишь выйдя за рамки А. л., в к-рой они, наоборот, приобретают вполне определ. смысл и, не отличаясь ничем от высказываний, соответственно, А->В и C->(C-^DE) при А = В = С=Л и £>=Е=И, являются даже истинными.

Это связано с др. важной стороной формализации в А. л.— требованием, чтобы операции задавались таблично как функ­ции, т. е. чтобы значение сложного высказывания зависело только от значений составляющих его простых высказываний. Так, конъюнкция задается таблицей: И • и = И, ИЛ=Л, Л ■ Л=Л, Л • Л=Л; дизъюнкция — таблицей: И\ И = И, И\/Л = И, ЛУИ=И, ЛVЛ=Л; импликация — таблицей: И->И = И, И->Л=Л, Л-+И = И, ЛнЛ=И (эта таблица вы­текает из требования табличное™ операции и естеств. требо­ваний, чтобы были такие случаи, когда А-^В ложно, но чтобы все частные случаи такого высказывания, как «Если х=2, то х-=4»,были истинны; случаи, когда х принимает одно из зна­чений 2,—2,1,как раз и дают три из четырех равенств таблицы); эквиваленция — таблицей: И~И = И, И~Л=Л, Л~И=Л, Л~Л = И; отрицание—таблицей: И=Л, Л = И. Эти таблицы позволяют вычислять значения сложных высказываний, зная значения простых.

Осн. суть А. л. как системы методов состоит в использо­вании преобразований высказываний на основе тех алгебраич. законов, к-рые имеют место для операций над высказывания-

АЛГЕБРА ЛОГИКИ 35

ми. Эти законы чаще всего имеют вид тождеств, т. е. равенств, верных при всех значениях переменных.

Важную роль играют следующие тождества:

этих операций и буквенные переменные. Именно, любую функ­цию Ф (А,, Ао,..., А₍₁) можно записать как дизъюнкцию всех выражений вида

 

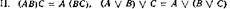
(законы коммутативности);

(законы ассоциативности);

(законы поглощения);

(закон дистрибутивности);

V. АА =.- Л

(закон противоречия);

(закон исключенного третьего;.

Эти тождества, устанавливаемые, напр., с помощью таб­лиц, позволяют уже без помощи таблиц получать др. тождества. При этом методом получения последних является метод тож­деств, преобразований (т. е. преобразований, к-рые, изменяя выражение, не изменяют при этом функцию, выражаемую последним), совершенно аналогичных тем, которые изучаются в школьном курсе алгебры (но основанных уже на новых тождествах).

Так получим, напр., законы идемпотентности: АА=А, А\А~А [последний доказывается так:

г. е. с использованием лишь (обоих) законов по­глощения]; 2-й закон дистрибутивности А\/ВС= (AVB) (АуС) [доказательство: А у ВС = А У АС У ВС= = А V САу СВ = А(А V В)уС(АуВ) = (АуВ)Ау(АуВ)С =

■- (А\В)(А\/' С)]; двойного отрицания закон А~А [доказа­тельство: A =liCA\J А) —'А • И = 1(ДУА) = А~А\АА =. \A\~aA = АА\ Л = АА~уАА~= А (АуА) = А(А~уА1=А • И = А(АуА) =А]\ законы де Моргана: АВ = АуВ, А\ В=АВ; законы зачеркивания: AV АВ = А у В, А(А у В)_= АВ; законы выявления: АВ\АС =АВ\АС\ ВС, (Ау В)(Ау С) = ■-(А\В)(А\ С)(В\ С). Вообще тождеств I—VI достаточно для того, чтобы из них по методу тождеств, преобразований можно было вывести всякое (верное, конечно) тождество, левая л правая части к-рого —выражения А. л., состоя­щие из переменных А, В,.-., констант и, Л и знаков<<•», «.,», «—» (не обязательно включая все из них). Добавление н;е тождеств VII А-*\В=АуВ, А~В=АВуАВ дает воз­можность выводить и любые тождества, содержащие также зна­ки*^», «-». Напр., такие: А->(В->С)=АВ^С (закон объеди­нения посылок), А(А-'В)— АВ (закон зачеркивания посылки),.1-В = В~»А (закон контрапозиции) А~В = А~В (закон

четностиэквиваленции), А-*А—И, А~А = И,А-^А~А,А~А = ^Л,А~В = (А^В). (В^А), А\/(В~С)= (AvB)-(AyO и др. Использование иеречисл. тождеств позволяет уже без большого груда выводить и мпогочисл. гораздо более сложные тождества, например (A-(B-(C—(D^£))))-*(A-.(B- (C-*(D->r))))=A-(£->

(C-(£>->(£->F)))),(A~B) -((C^-iJ) -*(E~(F~GJ)) = U~B)(.C~ £>)-*

-*{E~(F~G)),AB \>AC У ВС V DE\J DFyEFyADyBE\/CF= И, проверять к-рые непосредственно по таблицам было бы уже До­вольно трудно.

В записи последнего из этих тождеств существ, роль играет использование закона ассоциативности дизъюнкции, к-рый по­зволяет обходиться без скобок при записи выражения, к-рое можно понимать как дизъюнкцию неск. выражений (членов), т.е. такую же роль, какую в обычной школьной алгебре играет закон ассоциативности сложения (сочетательной закон) при записи суммы неск. слагаемых. Аналогичное можно сказать и о законе ассоциативности конъюнкции. Можно вывести также закон ассоциативности эквивалентности. Однако свя­занное с ним понятие эквиваленции нескольких переменных надо не путать с (попарной) эквивалентностью их. Так, А-В-С [т. е. (А~В)~С\ и (А~ В) (В - С) [т. е. попарная аквпвалентность] выражают различные функции [напр., Л-Л-Л =(Л~Л)~Л= И~Л = Л, но(Л~ Л) (Л~Л)=11 • И = = 1! J. Здесь сказывается различие между операцией эквивален-шш и отношением эквивалентности, хотя это, казалось бы, и одно и то же. Тем более следует соблюдать осторожность при сопоставлении эквиваленции неск. выражений, напр. vi~SB~(s,c их равенством vi — Ь = Ч, т. к. последнее означает именно попарное равенство (VI = 8 и!' = G); необходимо либо стро-ю различать эквиваленцию и равенство, либо, в случае их отождествления, избегать, напр., опускания скобок по ассо­циативности.

Тождества V, VI, VII показывают, что константы И и Л, импликацию и эквиваленцию, рассматривая их как функции, можно выразить через конъюнкцию, дизъюнкцию и отрицание. Более того, имеет место теорема, гласящая, что всякая функ­ция А. л. может быть представлена через эти три операции, г. е. записана в виде выражения, содержащего лишь знаки

где а,, ее,,..., а?? —набор из значений И, Л. Заменяя в этой дизъюнкции выражения А.; ~ И на А/, а А1 — Л — на л(, а

также стирая «коэффициенты» Ф(а,,а,..................... а.,),равные И(позакону

И-А=А) и отбрасывая члены с «коэффициентами», равными Л (позаконам (Л А = Л, Л\А=А), мы и получим (если функция не есть константа) то выражение, о к-ром говорится в теореме. Последнее наз. совершенной дизъюнктивной нормальной формой функции Ф(А,,...,А₍₁).

Дизъюнктивной нормальной формой (короче, днф) наз. выра­жение, к-рое есть буква И или Л или имеет вид VI,у й_ау...у'ь. где каждый член VI; является либо буквенной переменной, либо ее отрицанием, либо конъюнкцией таковых, причем s не обяза­тельно отлично от 1, т. е. знаков «у» может и не быть. Примеры днф: А,~В,^АВС,^АВ\С~, ААуС~С, АВАС\ ВСВ, ABCD\Ay V-Dy СЕ, ABCD\ ABCD\ ABCU,U, Л. Последние из этих днф являются т. н. совершенными. Днф наз. совершенной, если она есть и или Л или в каждом члене содержит ровно по одному ра­зу все имеющиеся в ней буквы (переменные) и не имеет оди­наковых членов. (Два выражения наз. одинаковыми, если одно из другого можно получить с помощью одних лишь за­конов коммутативности и ассоциативности). Всякое выражение А. л. можно привести (преобразовать) к днф. Для этого доста­точно элиминировать (т. е. исключить) константы и знаки опе­раций, отличных от конъюнкции, дизъюнкции и отрицания, выразив их через эти операции (напр., по V, VI, VII), а затем «спустить внутрь» (по законам де Моргана) все знаки отрицания, стоящие над сложными высказываниями, ликвидировать крат­ные отрицания (по закону ~Я=А) и, наконец, раскрыть все скоб­ки но закону дистрибутивности (при использовании также зако­нов ассоциативности и коммутативности). А всякую днф можно привести к совершенной днф, «домножая» члены на недоста­ющие буквы (по закону А=АВ\АЬ) и ликвидируя повто­рения букв в членах (по законам АА—А, АА =Л, Л-А=Л Л\/А=А) и повторения членов (по закону A vA=A).

Приведение к совершенной днф лежит в основе одного из алгоритмов для решения по любым двум данным выражениям VI и!В вопроса о том, одну ли и ту же функцию они выражают, т. е- верно ли тождество Vi= i ■ Алгоритм этот состоит в следую­щем: приводим;. и 25 к совершенным днф, содержащим все те переменные, к-рые есть в 'л, и все те, к-рые есть в а*, и смотрим, одинаковы ли эти две совершенные днф; если одинаковы, то ответ положителен, если нет — отрицателен. Однако совершен­ная днф, находя применение и к др. задачам, является все же часто весьма громоздкой. Поэтому приходится нередко пользо­ваться др. нормальными формами.

Из них важную рольиграетт. н. сокращенная днф. Послед­нюю можно определить как такую днф, в к-рой 1) нет повто­рений букв ни в одном члене, 2) нет таких пар членов 81; и vi: что всякий множитель из VI/ имеется и в Sly, и 3) для всяких двух таких членов, из к-рых один содержит множителем нек-рую букву, а другой—отрицание той же буквы (при условии, что другой буквы, для к-рой это же имеет место, в данной паре членов нет), имеется (в этой же днф) член, равный конъюнкции остальных множителей этих двух членов. Всякую днф можно привести к сокращенной днф путем конечного числа выбрасы­ваний членов по закону поглощения (ср. с условием 2) и добав­лений членов по закону выявления (ср. с условием 3) с исполь­зованием также нек-рых более простых законов (коммутатив­ность, ассоциативность, А=А-И) и ликвидацией повторений букв в членах и повторений членов. Пример пр иведения выраж е-

ния к сокращенной_днф: (А~(В-+С))~>АС=А(В\/С)\~АВ\_Су УАС = (А\ ВСУ.А\В X_OVAC=AA\ АВ \ АСУ ВСА\ ВСВ V У ВССу[АС=31\АВ\ АС\ ВСА\ Л\_ЛУАС=АВУ ВСА\_АСУ УАС = АВУ ВСАу АСУ АС\ С=АВ У СВ А\ С = АВ^\СВАу \'С-Я= АВУСВА\>С1Л\ВА-М = АВУСУВА V ВАС = ABV УСУ ВА. Тождество VI =!В верно, если, и только если, получа­емые из 'Л и Ь сокращенные днф одинаковы.

Кроме Днф, употребляются также конъюнктивные нормаль­ные формы (кнф). Это такие выражения, к-рые можно получить из днф путем замены в них знаков «\» на «•», а «■» на «у». [Пример кнф А(В\ CV-DXAV D) ]. Конечно, такое преобразова­ние не является тождественным, т. е. может изменить функцию, выражаемую данной днф. Оно есть преобразование двойствен­ности.

Преобразованием двойственности наз. такое преобразование выражения А. л., при к-ром в этом выражении знаки всех one раций заменяются на знаки двойственных им операций, а кон­станты: И на Л, Л на И; причем операция (или функция) Ф Has. двойственной для операции ч~,если таблица, задающая ф, полу­чается из таблицы, задающей V, путем замены в ней всюду И на Л, а Л на И (имеется в виду одновременная замена и значений функции, и значений ее аргументов). Если Ф двойственная ч, а V двойственная у, ^{т0 ф} — Х- Напр., конъюнкция и дизъюнк­ция двойственны между собой, отрицание двойственно самому себе, константа И (как функция) двойственна константе Л.

36 АЛГЕБРА ЛОГИКИ

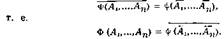
Функция Ф(А,............. А) двойственна функции Ч' (Аи...,Ап), если, и только если, верно тождество

Если верно тождество 51 = SB и 81* двойственно а, a SB* двойственно S>, то верно и тождество 81* = si'*, называемое двойственным пре­дыдущему тождеству. Это — т. н. принцип двойственности. При­мерами двойственных тождеств являются пары законов I, II, III и др.; тождество V двойственно тождеству VI.

Совершенную кнф и сокращенную кнф можно определить как такие кнф, что двойственные им выражения есть, соответст­венно, совершенная днф и сокращенная днф. Совершенные и сокращенные днф и кнф можно использовать для решения задачи обзора всех гипотез и всех следствий данного выражения А. л. Причем под гипотезой выражения 81 А. л., т. е. в условиях принятых в ней абстракций, естественно понимать такое выраже­ние $?, что Я-»И тождественно истинно, т. е. истинно при всех значениях переменных высказываний; а под следствием выра­жения л — такое выражение S.4 что si-* S3 тождественно истинно. Гипотеза выражения 81 наз. простой, если она есть конъюнкция буквенных переменных или их отрицаний и после отбрасывания какого бы то ни было из этих ее множителей перестает быть ги­потезой выражения 81. Аналогично, следствие выражения 81 наз. простым, если оно есть дизъюнкция букв или их отрицаний и после отбрасывания какого бы то ни было из ее членов пере­стает быть следствием выражения 81. Решение задач обзора гипотез и следствий основано на следующих теоремах. 1° Если 81 = SB, то у 81 и у 5В одни и те же гипотезы и одни и те же след­ствия. 2° Каждый член днф является гипотезой этой днф. 3° Каждый множитель кнф есть следствие этой кнф. 4° Если S3 — гипотеза выражения 81, то S35 — тоже гипотеза выражения 81. 5° Если SB — следствие выражения Si, то 83 V ® — тоже след­ствие выражения 91. 6" Если S3 и е — гипогезы выражения S3, то S3 V S—тоже гипотеза выражения 81. 7^и Если S3 и 6 —след­ствия выражения 81, то S^;©— тоже следствие выражения 81. 8^е У совершенной днф нет других гипотез (не содержащих букв, не входящих в эту днф), кроме дизъюнкций (нек-рых) ее членов или тождественно равных им (т. е. равных при всех значениях переменных) выражений. 9'- У совершенной кнф нет других следствий, кроме конъюнкций (нек-рых) ее множителей или тождественно равных им выражений. 10° Сокращенная днф есть дизъюнкция всех своих простых гипотез. 11^е Сокращенная кнф есть конъюнкция всех своих простых следствий. Из обзора же простых гипотез и следствий нетрудно получить (пользуясь 2°—7^ и обзор всех остальных гипотез и следствий.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: