 |
Метод синтеза В.В. Солодовникова для следящих систем с астатизмом первого порядка.
|
|
|
|
В основу синтеза положены следующие показатели качества:
перерегулирование 
при единичном ступенчатом воздействии на входе;
время переходного процесса 
;
коэффициенты ошибок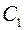 
и 
.
Типовая вещественная частотная характеристика замкнутой системы 
(рис. 1) описывается следующими величинами:
- основной коэффициент наклона; 
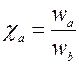и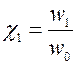 
- дополнительные коэффициенты наклона; 
и 
- основной и дополнительный коэффициенты формы; 
- интервал положительности.
Рис. 1
На основании заданного перерегулирования можно определить 
, затем по зависимость между временем переходного процесса и частотой , соответствующей интервалу положительности вещественной характеристики.
После нахождения основных величин для типовой вещественной характеристики (по таблице) переходят к формированию желаемой логарифмической амплитудной характеристики. При этом очевидно, что фазовая характеристика разомкнутой системы должна так проходить, чтобы обеспечивалась не только устойчивость, но и определенный запас устойчивости.
Вещественная характеристика замкнутой системы связана с частотной передаточной функцией разомкнутой системы 
зависимостью
. (4)
Задаваясь различными значениями 
, на комплексной плоскости можно построить кривые, дающие связь между вещественной и мнимой частями или между ее модулем и фазой (или запасом по фазе). На рис. 3 приведено подобное семейство кривых для амплитуды, откладываемой в децибелах.
Кривые, приведенные на рис. 3, позволяют сформулировать требования к амплитудно-фазовой характеристике разомкнутой системы, которые необходимо выполнить, чтобы обеспечить получение желаемой типовой характеристики.
|
|
|
На рис. 4 построены кривые, которые позволяют при заданном значении перерегулирования выбирать требуемое значение запаса по модулю 
и запаса по фазе 
.
Рис. 4
Первая низкочастотная асимптота проводится так, чтобы она имела наклон 
, соответствующий астатизму первого порядка (рис. 5). Продолжение асимптоты должно пересечь ось частот при частоте, равной желаемой добротности по скорости:
,
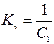где 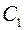- заданный коэффициент ошибки.
При однократном изломе в точке B первая сопрягающая частота определяется по формуле
(5)
где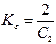 
- добротность системы по ускорению, а при двукратном изломе - по формуле
. (6)
Рис. 5
Далее по найденной из рис. 2 частоте положительности определяется частота среза л. а. х. 
так, чтобы она удовлетворяла условию
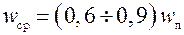(7)
Среднечастотный участок желаемой л. а. х. образуется асимптотой с наклоном — , проводимой так, чтобы она пересекала ось частот при . Этот участок проводится влево и вправо до достижения модулей,. равных 
(рис. 5). Затем производится сопряжение среднечастотного участка с низкочастотными асимптотами и высокочастотной частью.
Передаточные функции и л. а. х. всех четырех типов полностью определяются заданием четырех величин: коэффициента усиления 
и трех сопрягающих частот 
(рис. 6). Л. а. х. полностью определяется также заданием следующих четырех величин: коэффициента усиления в децибелах 
при частоте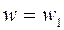 
, частоты среза и двух относительных сопрягающих частот 
и 
.
Рис. 6
После формирования всей желаемой л. а. х. необходимо проверить, выдерживается ли требуемое значение запаса по фазе, определяемое из графика на рис. 4 для модулей, лежащих в пределах
. (9)
Для этой проверки, необходимо подсчитать фазовый сдвиг в двух крайних точках среднечастотного участка, имеющего наклон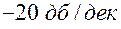 
, т. е. при частотах 
. Подсчет фазового сдвига делается на основании принятой желаемой передаточной функции. Например, для передаточной функции типа I (см. табл. 2) он равен
|
|
|
.
Если требуемый запас по фазе не выдержан, то необходимо расширить среднечастотный участок и произвести вновь проверку.
Далее из ординат желаемой л. а. х. вычитаются ординаты располагаемой л. а. х. Получившаяся л. а. х. соответствует передаточной функции последовательного корректирующего звена. При необходимости это звено может быть пересчитано на эквивалентную обратную связь или эквивалентное параллельное корректирующее звено.
Случайные процессы.
Изменение во времени 
случайной величины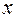 
называется случайным или стохастическим процессом. Случайный процесс - множество возможных кривых 
, так как случайная величина не имеет определенного значения, а является совокупностью (множеством) возможных значений.
Случайный процесс (СП) может быть оценен некоторыми вероятностными характеристиками. В каждый отдельный момент времени 
наблюдаются случайные величины 
, каждая из которых имеет свой закон распределения
Рис. 5
Для каждого заданного момента времени можно найти характеристики случайных величин: среднее по множеству (математическое ожидание)
(1)
и дисперсию
(2)
Среднее значение случайного процесса представляет собой некоторую среднюю кривую (рис. 5), около которой группируются все возможные отдельные реализации этого процесса, а дисперсия 
или среднеквадратичное отклонение 
характеризуют рассеяние отдельных возможных реализаций процесса около этой средней кривой.
Среднее значение случайной величины 
для отдельной реализации случайного процесса определяется из выражения
(3)
Чисто случайный процесс: все значения случайной величины в отдельные моменты времени не зависят друг от друга. Вероятность их совместного наступления равна произведению вероятностей наступления каждого из них в отдельности:
(4)
где 
- значения с.в.
Если события зависимы, то учитывается взаимозависимость или корреляцию между ними: вместо формулы (4) записывается
(5)
где 
- условная вероятность того, что случайный процесс пройдет вблизи точки 
, если он уже прошел через точку 
. Следовательно, зная плотности вероятности 
можно найти также и условную плотность вероятности
(6)
|
|
|
Стационарным случайным процессом называется такой процесс, вероятностные характеристики которого не зависят от времени. Все плотности вероятностей 
не меняются при любом сдвиге рассматриваемого участка процесса во времени
Свойства стационарного случайного процесса (ССП):
1. Исследование стационарного случайного процесса позволяет определить только установившиеся (стационарные) динамические ошибки САУ систем при случайных воздействиях.
2. Свойство эргодической гипотезы: с вероятностью, равной единице всякое среднее по множеству равно соответствующему среднему по времени, в частности 
, 
и т. д.
Эргодическая теорема: среднее значение (математическое ожидание) для ССП равно
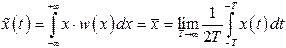(8)
Также определяются дисперсия, среднеквадратичное отклонение и т. п. Эргодическая гипотеза позволяет упрощать все расчеты и эксперименты: для определения 
и т. п., вместо параллельного испытания многих однотипных систем в один и тот же момент времени, можно пользоваться одной кривой 
, полученной при испытании одной системы в течение длительного времени.
Таким образом, отдельная реализация ССП на бесконечном промежутке времени полностью определяет собой весь процесс со всеми бесчисленными возможными его реализациями.
|
|
|
