 |
Частотные методы оценки качества переходных процессов в САУ
|
|
|
|
Допустим, что выходной сигнал следящей системы в любой момент времени точно копирует входной. Тогда передаточная функция замкнутой системы 
, и соответствующая амплитудно-фазовая характеристика также равна единице: 
. Следовательно, амплитудно-частотная и фазово-частотная характеристики соответственно будут равны: 
.
Другими словами, на всех частотах вынужденных колебаний амплитуда выходного сигнала равна амплитуде входного и сдвиг фаз между ними равен нулю (рис. 1, а). Однако равенство 
может выполняться лишь в идеальном случае, если все элементы системы безынерционны. Поэтому ввиду инерционности системы, которая отражается постоянными времени ее звеньев, амплитудная 
и фазовая 
частотные характеристики замкнутой системы обычно имеют вид, приведенный на рис. 1, б.
В этом случае условия 
и 
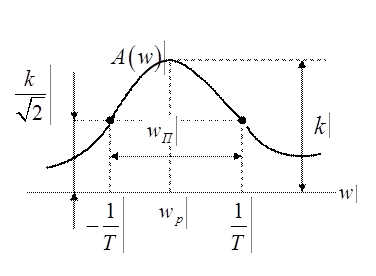
выполняются на небольшом участке малых частот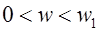 
(заштрихованный участок на рис. 1, б). На резонансной частоте 
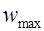амплитудная характеристика имеет максимум 
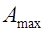. При дальнейшем увеличении частоты система вследствие своей инерционности не успевает реагировать на колебания больших частот, и 
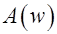резко падает. Фазовая частотная характеристика отрицательна. Следовательно, выходной сигнал отстает по фазе от входного. По своим частотным свойствам следящая система может быть отнесена к классу фильтров нижних частот, которые хорошо пропускают колебания малых частот и плохо — больших.
Установлено, что чем больше 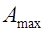, тем более колебательным является переходный процесс. Поэтому отношение 
называют показателем колебательности - показатель колебательности (
- отношение максимального значения амплитудной частотной характеристики к ее значению при 
).
|
|
|
Для следящих систем 
, поэтому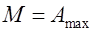 
. Обычно 
. При малых система «вялая» и имеет большое время регулирования. При больших увеличивается перерегулирование, и система приближается к границе устойчивости.
Кроме частоты 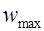характерными частотами амплитудно-частотной характеристики являются 
. Частота 
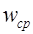называется частотой среза замкнутой системы и определяется на уровне 
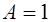(частота среза 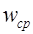- частота, при которой 
). Для следящих систем частота 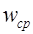определяет диапазон частот вынужденных колебаний, которые пропускает система без ослабления. На этой частоте амплитуды входного и выходного колебаний равны между собой.
Частота 
называется полосой пропускания замкнутой системы и определяется на уровне 
(полоса пропускания - это интервал частот от 
до 
, при котором соблюдается условие: 
).
Так как в диапазоне частот 
амплитудная характеристика резко падает, то числовые значения частот 
близки друг к другу.
Полоса пропускания влияет на точность и быстродействие системы. С увеличением полосы пропускания быстродействие системы увеличивается. Чем больше полоса пропускания, тем больший спектр входного сигнала передается системой без искажений. Следовательно, точность отработки входного сигнала повышается. Однако, при наличии высокочастотных помех во входном сигнале САУ одинаково хорошо пропускаются и сигналы и помехи.
Резонансная частота системы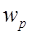 
- частота, при которой амплитудная характеристика имеет максимальное значение.
Таким образом, показатель колебательности и полоса пропускания являются косвенными показателями качества переходного процесса.
Интегральные оценки
Прямые показатели качества переходного процесса характеризуют отдельные его стороны. Возникает вопрос: нельзя ли переходный процесс оценить только одним обобщенным критерием без непосредственного определения его отдельных показателей? Оказывается, можно. Таким обобщенным критерием является интегральная оценка переходного процесса.
|
|
|
Интегральная оценка представляет собой определенный интеграл от некоторой функции переходной составляющей ошибки. Обычно интегральные оценки применяют для следящих систем, которые являются астатическими. В этих системах установившаяся ошибка при ступенчатом задающем воздействии равна нулю, и переходная составляющая ошибки равна ошибке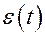 
системы: 
.
В общем виде формула для определения интегральной оценки имеет вид:
(1)
Простейшей интегральной оценкой является интеграл
(2)
Однако эта оценка может быть применена только для переходных процессов без перерегулирования, когда ошибка не меняет своего знака (рис. 1, а). Интеграл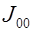 
определяет заштрихованную площадь на рис. 1, а, которую иногда называют площадью регулирования.
При колебательном характере переходного процесса оценка 
не может быть применена, так как ошибка 
имеет разные знаки. В этом случае применяют интегральную оценку (рис. 1, б),
но вычисление интеграла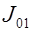 
весьма затруднительно.
Для оценки как колебательных, так и монотонных переходных процессов предложена и часто применяется квадратичная интегральная оценка, которая не зависит от знака ошибки, а значит, и от характера кривой переходного процесса
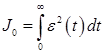
Интеграл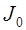 
определяет заштрихованную площадь под кривой, 
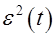которую иногда называют квадратичной площадью регулирования (рис. 2). Величина интеграла 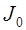будет тем меньше, чем меньше сумма заштрихованных площадей на рис. 2, т. е. чем ближе переходной процесс к идеальному ступенчатому изменению регулируемой величины, вызванному ступенчатым изменением задающего воздействия.
В результате приближения переходного процесса к идеальному (ступенчатому) получается большая скорость – 
процесса при подходе регулируемой величины к новому установившемуся значению, что вызывает большое перерегулирование.
Поэтому при оценке переходного процесса по интегралу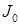 
сильно колебательный процесс может оказаться лучшим, чем не колебательный, а это не всегда является правильным. Квадратичную интегральную оценку 
можно улучшить, если учитывать не только ошибку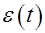 
, но и скорость ее изменения 
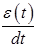. Такой оценкой является интеграл 
.
|
|
|
Можно доказать, что минимум интегральной оценки 
соответствует приближению переходного процесса не к ступенчатому, а к некоторому экспоненциальному процессу с постоянной времени 
(пунктирная кривая на рис. 3, которую называют экстремалью). Выбор параметров системы из условия 
соответствует менее колебательному процессу по сравнению с использованием квадратичной оценки 
.
Находят применение и более сложные интегральные оценки, учитывающие ошибку 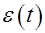, а также первую 
, вторую 
и более высокие производные от 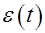. При любых интегральных оценках качество переходного процесса будет тем лучше, чем меньше величина соответствующего интеграла.
Интегральные оценки вычисляют через коэффициенты изображения ошибки.
Рис. 3. Переходный процесс, соответствующий минимуму интегральной оценки
Выводы. Качество процессов регулирования — это обобщенная характеристика динамических свойств автоматических систем, которая определяется поведением САУ как в переходных процессах, так и в установившихся режимах.
Переходный процесс обусловливается инерционностью системы. Его можно оценить прямо или косвенно. При прямой оценке тем или иным способом строят график переходного процесса, по которому находят основные его показатели. Косвенные оценки не требуют построения графика переходного процесса, и в этом их достоинство. Они позволяют определить некоторые черты переходного процесса и установить влияние параметров системы на качество переходных процессов, однако при этом ухудшается устойчивость. Поэтому имеют место противоречивые требования к точности и устойчивости.
Показатели качества процесса регулирования должны удовлетворять предъявляемым к системам требованиям. Это достигается коррекцией динамических свойств системы.
|
|
|
