 |
Ошибки влияния возмущения.
|
|
|
|
Для определения ошибок от возмущения структурную схему системы необходимо привести к виду, показанному на рис. 1, где Wp(р) и Wo(p) — передаточные функции частей системы, условно именуемых соответственно регулятором и объектом.
Передаточная функция по возмущению (рис. 1, б)
,
где W(р) = Wp(p) Wo(p) — передаточная функция разомкнутой системы.
Рис. 1. Структурные схемы САУ при наличии задающего и возмущающего воздействий (а) и только возмущающего воздействия (б).
Тогда изображение ошибки в соответствии с формулой (2)
(10)
Пользуясь этой формулой, можно не только вычислить величину установившейся ошибки, но и определить порядок астатизма системы по отношению к возмущению. Так, в частности, если регулятор не содержит интегрирующего звена, то система будет статической, если содержит — то астатической (рис. 2).
Например, при статическом объекте и статическом регуляторе соответственно имеем Wo(0) = k0 и Wp(0) = kp. При ступенчатом возмущении
f(t) = f0.. С учетом того, что F(р) = f0 /f(t) установившаяся ошибка будет равна
(11)
где 
- коэффициент передачи разомкнутой системы, т.е. система статическая.
Если же регулятор будет астатическим, т. е. 
, причем 
, то 
, (12)
т. е. система является астатической.
Точность автоматических систем характеризует вынужденное движение, которое оценивается величиной установившейся ошибки.
Точность автоматических систем характеризует вынужденное движение, которое оценивается величиной установившейся ошибки.
Эта ошибка зависит как от характера внешнего воздействия, так и от свойств самой САУ. С увеличением коэффициента передачи разомкнутой системы ее ошибки уменьшаются, однако при этом ухудшается устойчивость. Поэтому имеют место противоречивые требования к точности и устойчивости.
|
|
|
Показатели качества процесса регулирования должны удовлетворять предъявляемым к САУ требованиям. Это достигается коррекцией динамических свойств САУ.
33. Критерий инвариантности САУ.
Инвариантность(невозмущаемость) - означает в буквальном смысле неизменность.
Автоматические системы, в которых имеет место независимость какой-либо выходной координаты 
, в том числе и ошибки от внешнего возмущения 
, называют инвариантными.
При соблюдении условий инвариантности в САУ, т. е. когда она приобретает свойство независимости от возмущений, расширяется ее прикладной аспект и становятся оправданными теоретические гипотезы и предпосылки.
Рассмотрим систему уравнений, описывающих движение системы,
;
; (1)
Г. В. Щипанов считал, что для независимости координаты 
нужно, чтобы минор 
был тождественно равен нулю.
Действительно, если 
независимы, то при изменении 
на некоторую величину 
должны измениться координаты 
, а 
(она инвариантна от ) остается прежней. Иными словами, система
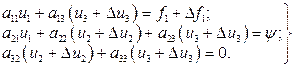(2)
и система (1) по 
дадут одинаковые решения.
Образуем третью систему, описывающую возмущенное движение остальных координат (над ):
Если принять все три величины 
за переменные, то однородная система только тогда даст отличное от нуля решение (
), когда определитель тождественно равен нулю.
Итак, 
(по условию) и одно из неравенств 
(или оба сразу) должны выполняться, когда
Отсюда очевидно, что условие
(3)
является условием независимости 
.
После этого легко получить правило для определения условия инвариантности. Для этого в определителе системы (1) нужно вычеркнуть строку, в которой стоит возмущение, и столбец, в котором стоит интересующая нас координата. Оставшийся минор и есть искомый минор Г. В. Щипанова.
В любом другом общем случае координата 
будет независимой от 
, (при условии независимости 
между собой), если оставшийся после вычеркивания строки с и столбца с определитель будет равен нулю.
|
|
|
34. Условия физической реализуемости инвариантных САУ.
Если справедливы условия инвариантности и вследствие этого физически реализована независимость координаты относительно , то как бы не изменялось, в инвариантной системе никак не реагирует на это. Т. е. можно считать, что такой же эффект даст система с разорванными связями для передачи . Иными словами, система, разомкнутая в точке выхода по всем побочным связям (все 
, исключая 
, равны нулю), равноценна исходной инвариантной системе. Уравнение процессов в разомкнутой системе (для того же исходного случая)
;
; (4)
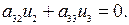
Решение системы возможно, если
(5)
Это и есть условие физической реализуемости в форме Петрова-Кухтенко.
Однако получилось противоречие. С одной стороны, для того, чтобы система была инвариантной, должно выполняться равенство
,
с другой стороны, для ее физической реализуемости необходимо, чтобы
Приходим к выводу: при малом 
должно быть большим 
. А что это значит? Усиление самого объекта должно быть настолько малым 
, что возмущение 
на координату не доходит.
Таким образом, и создание за малое время бесконечных запасов энергии в регуляторе, и уменьшение (до нуля) чувствительности объекта к возмущению - трудно достижимые факторы.
35. Способы создания инвариантных САУ.
Первым решением проблемы физически реализуемых инвариантных систем явилось применение комбинированного управления.
Суть этого способа состоит в том, что нужно измерить (непосредственно или косвенно) возмущение и организовать новое управление на объект (новый канал). Дополним схему (рис. 1) таким регулятором (рис. 3).
На схеме (рис. 3) поставили измеритель и стали формировать 
(сделали зависимым и 
). Уравнение (1) теперь можно записать так:
Считая независимым от и дадим приращения
Составляя возмущенное движение относительно координат 
и 
, получаем
(6)
Очевидно, что 
, если
Следовательно, условие инвариантности теперь будет записано в виде
(7)
Условие физической реализуемости САУ осталось прежним, так как при размыкании определитель эквивалентной системы остался тем же:
|
|
|
Хотя
выбором
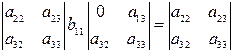
можно сделать систему абсолютно инвариантной.
Трудности измерения возмущения являются существенным фактором, стоящим на пути широкого применения принципов теории инвариантности для создания невозмущаемых систем.
Наряду с проблемой непосредственного замера актуальными стали вопросы косвенного измерения возмущения: путем обратного пересчета; заменой возмущения эквивалентным, но легко замеряемым; заменой возмущения эквивалентными начальными условиями; измерением второй производной от координаты (памятуя, что по закону Ньютона 
) и, наконец, применением принципа адаптации. Рассмотрим кратко, в чем сущность этих способов.
Пусть существует простейшая система автоматического регулирования, процессы в которой описываются уравнением
. (8)
Будем считать координатой, а 
возмущением. Вместо исходной системы автоматического регулирования возьмем следующую:
(10)
Замерив и задавшись 
, найдем в первоначальный момент 
.
Заведем 
в объект.
По полученной ошибке (недокомпенсации) можно вводить нужные коррективы в совершенство способа измерения приборного 
.
Рис. 4. Схема инвариантной системы с замером приборного 
.
Академик В.С. Кулебакин предложил оператор К (Д) - изображение, суть которого состоит в том, что если его применить к возмущению 
, то К (Д) 
.
Если применить к уравнению (8) это К (Д) изображение, получим эквивалентную систему
Так как операторы 
могут совпадать, то задача свелась к решению однородного уравнения более высокого порядка.
Решив это уравнение, найдем 
.
Сравнивая с 
, находим ошибку для исправления оператора.
Осуществляем подбор К(Д) и 
до тех пор, пока ошибка 
не будет равна нулю. По виду К(Д) из запасенных в генераторе возмущений выбираем , близкое к , и в противофазе к фактически существующему подаем на объект как компенсацию.
Движение тела происходит под влиянием силы. Но сила пропорциональна второй производной от координаты. Поэтому, измеряя ускорение движущегося тела и формируя 
, можно вводить компенсацию до того, как резко изменит характер движения.
|
|
|
36. Функции чувствительности временных характеристик.
Посредством этих функций чувствительности оценивается влияние малых отклонений параметров системы от расчетных значений на временные характеристики системы (переходную функцию, функцию веса и др.).
Пусть исходная система описывается совокупностью нелинейных уравнений первого порядка
(3)
Рассмотрим мгновенные вариации параметров 
, так что параметры приняли значения 
.
Тогда
(4)
Для дополнительного движения можно записать
(5).
Дополнительное движение можно разложить в ряд Тейлора.
Тогда получим уравнения первого приближения для дополнительного движения
. (6)
Частные производные, находящиеся в скобках, должны быть равны их значениям при 
.
Дифференцирование исходных уравнений (3) по 
приводит к так называемым уравнениям чувствительности
. (7)
Решение этих уравнений дает функции чувствительности 
. Однако уравнения (7) оказываются сложными и решение их затруднительно. Более целесообразен путь структурного построения модели, используемой для нахождения функций чувствительности.
В некоторых случаях функции чувствительности получаются дифференцированием известной функции времени на выходе системы. Так, если передаточная функция системы соответствует апериодическому звену второго порядка, то
.
При поступлении на вход ступенчатой функции 
на выходе будет
.
Пусть, например, вариацию претерпевает постоянная времени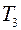 
. Тогда дифференцирование последнего выражения по 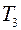даст функцию чувствительности по этому параметру
Дополнительное движение при этом будет 
, где 
- вариация постоянной времени .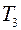
Пусть рассматриваемая система описывается совокупностью уравнений первого порядка
(8)
Уравнения чувствительности получаются из (8) дифференцированием по варьируемому параметру 
, от которого могут зависеть коэффициенты 
и 
:
(9)
где 
- и 
- частные производные от коэффициентов системы уравнений (8) по варьируемому параметру .
Для решения (9) необходимо предварительно решить совокупность уравнений (8) и определить исходное движение 
.
Для нахождения функций чувствительности и дополнительного движения удобно использовать передаточные функции системы. Пусть, например, регулируемая величина 
связана с задающим воздействием зависимостью
(10)
где 
- изображение задающего воздействия.
Функция чувствительности может быть получена из (10) дифференцированием по параметру :
,(11)
(12)
функция чувствительности передаточной функции, которая определяет первое приближение дополнительной передаточной функции, равной разности варьируемой и исходной передаточных функций при вариации параметра
|
|
|
|
|
|
