 |
Частотные критерии устойчивости.
|
|
|
|
В ходе функционирования САУ постоянно находится под воздействием возмущающих воздействий. Об устойчивости САУ к воздействиям помех можно судить по корням д.у.: если система устойчива, то корни д.у. отрицательны, а если корни комплексные, то отрицательными должны быть их действительные части.
Рассмотрим исходное д.у.:  (1) и его характеристическое уравнение
(1) и его характеристическое уравнение  (2) Пусть корни уравнения (2)
(2) Пусть корни уравнения (2)  , тогда уравнение (2) примет вид:
, тогда уравнение (2) примет вид:
 (3).
(3).
Критерий Михайлова позволяет оценивать не только устойчивость САУ, но и степень её устойчивости. Указанный метод основан на анализе корней характеристического уравнения  , но без их фактического вычисления.
, но без их фактического вычисления.
Для описания критерия Михайлова используется теория комплексных чисел вида  , где
, где  - действительная (вещественная) часть;
- действительная (вещественная) часть; 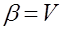 - мнимая часть. Для исследования устойчивости САУ удобно использовать графики, на которых по оси абсцисс откладываются значения вещественной части
- мнимая часть. Для исследования устойчивости САУ удобно использовать графики, на которых по оси абсцисс откладываются значения вещественной части  , а по оси ординат – значения мнимой части
, а по оси ординат – значения мнимой части 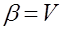 (рис. 1). Комплексное число можно представить в виде
(рис. 1). Комплексное число можно представить в виде  , где
, где  - модуль комплексного числа или его длина
- модуль комплексного числа или его длина  ,
,  - аргумент комплексного числа.
- аргумент комплексного числа.
 В характеристическом уравнении (3) заменим
В характеристическом уравнении (3) заменим  на
на  и получим:
и получим:

 Каждая из скобок представляет собой комплексное число и, следовательно,
Каждая из скобок представляет собой комплексное число и, следовательно,  представляет собой произведение
представляет собой произведение  комплексных чисел. При перемножении аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектора
комплексных чисел. При перемножении аргументы комплексных чисел складываются. Поэтому результирующий угол поворота вектора  при изменении
при изменении 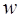 от
от  до
до  будет равен сумме углов поворота отдельных сомножителей
будет равен сумме углов поворота отдельных сомножителей 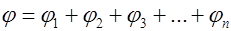
Критерий Михайлова предполагает изучение поведения вектора  при изменении частоты в диапазоне от
при изменении частоты в диапазоне от  до
до  , т.е.
, т.е. 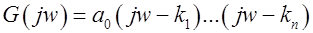 ,
,  .
.
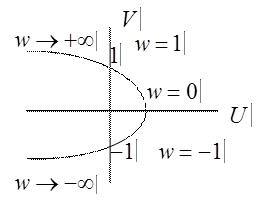
Пусть корень 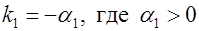 , тогда множитель будет иметь вид:
, тогда множитель будет иметь вид:  . Годограф этого вектора на комплексной плоскости при изменении
. Годограф этого вектора на комплексной плоскости при изменении 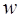 от
от  до
до  представлен на рис. 2 а).
представлен на рис. 2 а).
|
|
|
 |
При  вещественная часть
вещественная часть  , а мнимая
, а мнимая  . Таким координатам соответствует точка
. Таким координатам соответствует точка  на вещественной оси. При
на вещественной оси. При  вектор будет изменяться так, что его вещественная часть будет по-прежнему равна
вектор будет изменяться так, что его вещественная часть будет по-прежнему равна  , а мнимая часть
, а мнимая часть  , точка
, точка  на графике. При увеличении частоты до бесконечности конец вектора уходит в бесконечность, причем конец вектора все время остается на вертикальной прямой, проходящей через точку
на графике. При увеличении частоты до бесконечности конец вектора уходит в бесконечность, причем конец вектора все время остается на вертикальной прямой, проходящей через точку  . Вектор поворачивается против часовой стрелки, а результирующий угол поворота вектора
. Вектор поворачивается против часовой стрелки, а результирующий угол поворота вектора  .
.
Пусть корень  , тогда множитель будет иметь вид:
, тогда множитель будет иметь вид:  . Годограф этого вектора на комплексной плоскости представлен на рис. 2 б), а результирующий угол поворота будет равен
. Годограф этого вектора на комплексной плоскости представлен на рис. 2 б), а результирующий угол поворота будет равен  . Знак минус показывает, что вектор поворачивается по часовой стрелке.
. Знак минус показывает, что вектор поворачивается по часовой стрелке.
Пусть два корня, например,  представляют собой комплексные сопряженные величины с отрицательной вещественной частью т.е.
представляют собой комплексные сопряженные величины с отрицательной вещественной частью т.е.  . Сомножители, определяемые этими корнями, будут иметь вид
. Сомножители, определяемые этими корнями, будут иметь вид  . Проводя рассуждения, как и ранее для п.п. 1 и 2, получим, что результирующий угол поворота будет равен
. Проводя рассуждения, как и ранее для п.п. 1 и 2, получим, что результирующий угол поворота будет равен  .
.
Пусть те же комплексные корни имеют положительную вещественную часть, т.е.  , результирующий угол поворота будет равен
, результирующий угол поворота будет равен  .
.
Таким образом, если характеристическое уравнение будет иметь 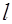 корней с положительной вещественной частью, то, каковы бы ни были эти корни (вещественные или комплексные), им будет соответствовать сумма углов поворотов, равная
корней с положительной вещественной частью, то, каковы бы ни были эти корни (вещественные или комплексные), им будет соответствовать сумма углов поворотов, равная  . Остальным
. Остальным  корням характеристического уравнения, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворотов, равная
корням характеристического уравнения, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворотов, равная  . В результате общий угол поворота вектора
. В результате общий угол поворота вектора  при изменении
при изменении 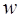 от
от  до
до  будет
будет
 .
.
Последним выражением и определяется искомая связь между формой кривой Михайлова и знаками вещественных частей корней характеристического уравнения: для устойчивости системы  порядка необходимо и достаточно, чтобы вектор
порядка необходимо и достаточно, чтобы вектор  при изменении
при изменении 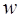 от
от  до
до  имел угол поворота
имел угол поворота  .
.
|
|
|
Для устойчивости системы необходимо, чтобы все корни лежали в левой полуплоскости, т.е. должно быть  .
.
Иная формулировка критерия Михайлова: для устойчивой САУ кривая Михайлова проходит последовательно  квадрантов, а корни уравнений
квадрантов, а корни уравнений  и
и 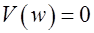 должны чередоваться. Кривая Михайлова всегда начинается с точки, расположенной на действительной оси, где мнимая часть обращается в нуль:
должны чередоваться. Кривая Михайлова всегда начинается с точки, расположенной на действительной оси, где мнимая часть обращается в нуль:  , то при постепенном увеличении частоты от нуля до бесконечности должна обратиться в нуль сначала вещественная часть:
, то при постепенном увеличении частоты от нуля до бесконечности должна обратиться в нуль сначала вещественная часть:  , затем мнимая:
, затем мнимая:  , затем опять вещественная и т.д. причем
, затем опять вещественная и т.д. причем  .
.
При четной степени уравнения кривая Михайлова стремится к бесконечности параллельно оси  и при нечетной степени - параллельно оси
и при нечетной степени - параллельно оси  . Пример. Исходное д.у.
. Пример. Исходное д.у.  . Построить годограф.
. Построить годограф.
Решение. Составим уравнение:  График годографа (рис. 3) показывает, что начало находится в точке
График годографа (рис. 3) показывает, что начало находится в точке  . Затем устремим
. Затем устремим 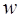 от
от  до
до  и получим
и получим
 .
.
 .
.
Система устойчива, так как годограф проходит все четыре квадранта.
|
|
|


