 |
Спектральная теория случайных процессов.
|
|
|
|
Рассмотрим так называемую энергетическую форму интеграла Фурье.
формула Релея (теорема Парсеваля), которая соответствует энергетической форме интеграла Фурье:
(5)
Подставляя 
, получим
(6)
Удобнее иметь дело не с энергией, а со средней мощностью процесса, которая будет получена, если энергию поделить на интервал наблюдения. Тогда формулу (5) можно представить в виде
(7)
Правая часть (7) представляет собой средний квадрат рассматриваемой величины х(t). Введем обозначение
, (8)
можно переписать формулу (7) в виде
(9)
или в виде
(10)
где 
или 
- спектральная плотность.
Важным свойством спектральной плотности является то, что интегрирование ее по всем частотам от 
до 
дает средний квадрат исходной функции времени х(t).
Физический смысл спектральной плотности – это величина, которая пропорциональна средней мощности процесса в интервале частот от 
до 
.
Спектральная плотность и корреляционная функция случайных процессов представляют собой взаимные преобразования Фурье, т. е. они связаны интегральными зависимостями:
; (11)
. (12)
Обычно спектральная плотность вычисляется по известной корреляционной функции при помощи формул (11). Эти формулы соответствуют так называемому двустороннему преобразованию Фурье четной функции времени 
.
Нормированная спектральная плотность является изображением Фурье нормированной корреляционной функции:
, (13)
где 
- спектральная плотность соответствует процессу 
и, следовательно,
(14)
где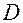 
- дисперсия.
Взаимные спектральные плотности 
и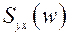 
являются изображениями Фурье 
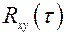и 
.
Рассмотрим некоторые стационарные случайные процессы, обладающие следующими свойствами: математическое ожидание равно нулю 
, а дисперсия 
. При этом средний квадрат случайной величины будет равен дисперсии: 
, а 
.
|
|
|
1. Белый шум. Под белым шумом понимается случайный процесс, имеющий «белый» спектр, т. е. одинаковое значение спектральной плотности при всех частотах от до (рис. 1): 
Примером такого процесса могут являться тепловые шумы сопротивления, которые дают уровень спектральной плотности хаотического напряжения на этом сопротивлении.
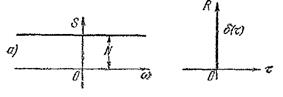
Рис. 1
2. Типовой входной сигнал следящей системы представлен на рис. 2. Скорость сохраняет постоянное значение в течение некоторых интервалов времени 
. Переход от одного значения к другому совершается мгновенно. Интервалы времени подчиняются закону распределения Пуассона, математическое ожидание 
, а средний квадрат скорости равен дисперсии, т. е. 
.
Среднее число перемен скорости за одну секунду- 
.
Среднее значение интервала времени, в течение которого угловая скорость сохраняет постоянное значение-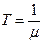 
Для определения корреляционной функции необходимо найти среднее значение произведения
.
При нахождении этого произведения могут быть два случая.
1. Моменты времени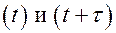 
относятся к одному интервалу. Тогда среднее значение произведения угловых скоростей будет равно среднему квадрату угловой скорости или дисперсии:
.
2. Моменты времени 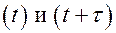относятся к разным интервалам. Тогда среднее значение произведения скоростей будет равно нулю:
,
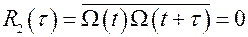так как произведения с положительным и отрицательным знаками будут равновероятными.
Корреляционная функция будет равна
где 
- вероятность нахождения моментов времени 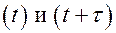в одном интервале,
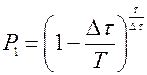
а 
- вероятность нахождения их в разных интервалах.
Устремив 
и переходя к пределу, получим
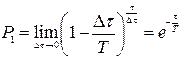
и окончательно 
. (15)
Спектральная плотность рассматриваемого процесса равна:
. (16)
3. Нерегулярная качка. Корабли, самолеты и другие объекты, находясь под действием нерегулярных возмущений (нерегулярное волнение, атмосферные возмущения и т. п.), движутся по случайному закону. Так как сами объекты имеют определенную, им свойственную, частоту колебаний, то они обладают свойством подчеркивать те частоты возмущений, которые близки к их собственной частоте колебаний. Получающееся при этом случайное движение объекта называют нерегулярной качкой в отличие от регулярной качки, представляющей собой периодическое движение.
|
|
|
Корреляционную функцию нерегулярной качки часто аппроксимируют выражением 
, а соответствующая спектральная плотность
где 
- дисперсия для угла, 
, 
.
При такой аппроксимации дисперсия для угловой скорости получается конечной: 
.
|
|
|
