 |
Классическая теория равновесного излучения
|
|
|
|
Первая проблема связана с теоретическим обоснованием равновесного излучения, возникающего внутри полости, окруженной со всех сторон непроницаемыми стенками, нагретыми до некоторой температуры 
(рис.1.1). Следует заметить, что небольшое отверстие, сделанное в стенке такой полости, можно рассматривать как абсолютно черное тело (Вин и Луммер, 1895г.)
Рис. 1.1.
Универсальность законов термодинамики обеспечивает применимость их как к веществу, так и к полю (как к классическим, так и к квантовым системам). В применении к равновесному излучению термодинамика позволила установить следующее:
1. Закон Кирхгофа, согласно которому отношение лучеиспускательной способности тела, к его поглотительной способности при данной температуре, не зависят от физических свойств тела и равно лучеиспускательной способности абсолютно черного тела, т.е. является универсальной функцией температуры и частоты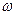 
(1859г.).
2. Существование светового давления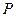 
излучения (величину светового давления легко найти, исходя из законов электродинамики: 
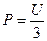, где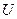 
– плотность энергии излучения).
3. Закон Стефана – Больцмана[1] о зависимости плотности энергии от температуры:
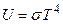, (1.1)
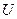отсюда на основе опытных данных для температуры и плотности энергии равновесного излучения вычисляют постоянную 
[2].
4. Закон Вина о спектральной плотности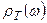 
равновесного излучения:
, (1.2)
вид функции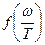 
остается термодинамически неопределенным.
5. Закон смещения Вина о том, что длина волны, соответствующая максимальной спектральной плотности энергии равновесного (черного) излучения, обратно пропорциональна абсолютной температуре:
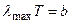, (1.3)
где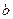 
- постоянная Вина.
Закон Вина (1.2) позволяет по заданной кривой распределения спектральной плотности энергии,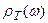 
при какой – либо температуре построить аналогичную кривую при любой другой температуре 
(рис. 1.2).
|
|
|
Формула Вина (1.2) автоматически приводит к закону Стефана – Больцмана (1.1):
,
Вводя новую переменную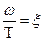 
, получим:
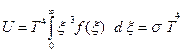. (1.1’)
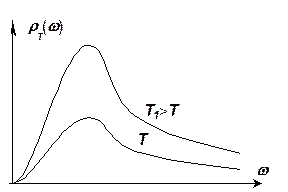
Рис. 1.2.
Таким образом, задача определения универсальной функции 
, с которой связанно теоретическое обоснование законов равновесного излучения, вышла на первое место в физике.
В классической физике эта задача решалась следующим образом. В полости кубической формы с ребром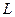 
существуют колебания всевозможных частот. В состоянии динамического равновесия колебания представляют суперпозицию стоячих волн. В декартовой системе координат, оси которой направлены вдоль трех ребер куба (рис. 1.3), условия существования стоячих волн записываются в виде:
, (1.4)
где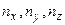 
– целые положительные числа.
Тогда число стоячих волн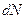 
, волновые числа которых заключены в интервале 
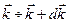, равно числу целых чисел в объеме 
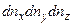, т.е.
. (1.5)
Переходя к сферическим координатам, где элементарный кубик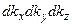 
(рис. 1.3) будет представлен элементарным объемом сферического слоя радиуса 
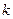и толщины 
в первом октанте (из-за целых положительных значений чисел 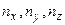), число стоячих волн 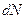в полости объема 
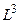перепишется в виде:
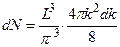. (1.6)
Рис. 1.3.
Подставляя соотношение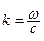 
в формулу (1.6.), получим для числа колебаний с частотой 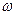из интервала 
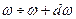в объеме 
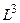полости формулу:
. (1.7)
Вейлем было показано, что это выражение справедливо независимо от формы полости и природы волн. Полное число электромагнитных колебаний следует увеличить в 2 раза за счет существования двух независимых поляризаций у поперечных волн:
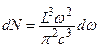. (1.8)
В первоначальных теориях число частот w из интервала 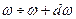, даваемое формулой Вейля (1.8), рассматривали как число осцилляторов оболочки полости, посылающих электромагнитные волны в полость объема .
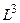Пользуясь этим представлением и рассчитав среднюю энергию линейного гармонического осциллятора на основе законов классической статистической физики, а именно, теоремы о равномерном распределении энергии по степеням свободы:
|
|
|
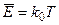. (1.9)
Релей и Джинс получили формулу для энергии излучения, с частотой 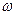, в полости в виде:
. (1.10)
Отсюда следует выражение:
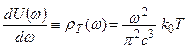, (1.11)
называемое формулой Релея – Джинса. Она удовлетворяет термодинамическому закону Вина (1.2), но резко противоречит эксперименту и закону Стефана – Больцмана. Действительно, плотность энергии равновесного излучения 
, но не 
.
Этот результат настолько противоречил эксперименту, что получил название «ультрафиолетовой катастрофы» (Эренфест, см. рис 1.4.)
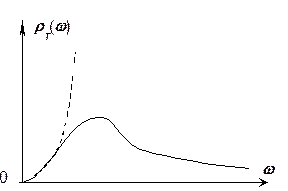
Рис. 1.4.
Возможен и другой подход к выводу формулы для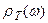 
в рамках классических представлений. Число колебаний 
с частотой 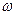, являющиеся носителями определенной энергии 
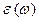, дается распределением Больцмана:
, (1.12)
где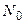 
– полное число носителей энергии. Отсюда для средней энергии колебаний с частотой 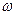оказывается равным
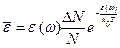, (1.13)
следовательно,
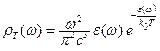, (1.14)
Вин на основе общих термодинамических соображений показал, что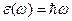 
, где 
- коэффициент пропорциональности. Тогда формула Вина принимает вид:
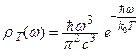. (1.15)
Этот закон Вина выполняется хорошо лишь для достаточно больших частот излучения.
Таким образом, формулы Релея – Джинса и Вина описывались лишь концы спектра равновесного излучения (абсолютно черного тела).
Нужны были новые идеи для создания более общей и строгой теории, объясняющей законы равновесного излучения (1.1), (1.2), (1.3) и разрешающей проблему с «ультрафиолетовой катастрофой».
Гипотеза Планка. Формула Планка. Фундаментальная
Постоянная Планка.
В 1900 г. М. Планк, анализируя опытные данные по излучению абсолютно черного тела, выдвинул гипотезу, которая коренным образом изменила представление классической физики. Согласно этой гипотезе осцилляторы (атомные системы) не могут иметь произвольную энергию; колеблясь с частотой 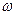, энергия осциллятора должна быть кратной некоторому минимальному значению 
, т.е.
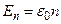, (1.16)
где 
=0,1,2,3,... Указанная совокупность энергий образует бесконечный, но дискретный ряд величин. Тогда средняя энергия осциллятора легко рассчитывается по формуле среднего статистического
|
|
|
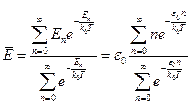. (1.17)
Обозначив 
, формулу (1.17) преобразуем к виду:
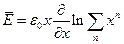. (1.18)
Вычисляя сумму 
, получим
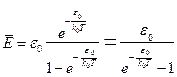. (1.19)
Это и есть формула Планка для средней энергии линейного осциллятора. Спектральная плотность энергии равновесного излучения в этом случае оказывается равной:
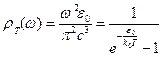. (1.20)
Чтобы формулу (1.20) привести в соответствии с термодинамической формулой Вина (1.2), Планк положил минимальную порцию энергии равной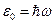 
, и получил знаменитую формулу[3]:
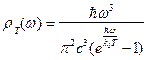, (1.21)
величина 
, имеющая размерность действия, называется постоянной Планка.
В случае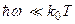 
(низкие частоты) имеем 
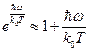и формула (1.21) переходит в формулу Релея – Джинса (1.11).
Если же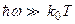 
(высоки частоты) формула (1.21) переходит в формулу Вина (1.15), т. к. 
.
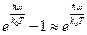Формула Планка (1.21), описывающая зависимость спектральной плотности равновесного излучения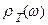 
от частоты 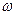, находится в блестящем согласии с экспериментом.
На основе формулы (1.21) легко найти плотность равновесного излучения:
.
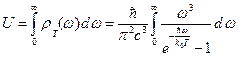Вводя новую переменную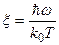 
, откуда 
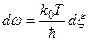, и учитывая табличный интеграл
,
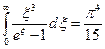получаем закон Стефана – Больцмана:
,
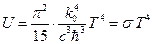где постоянная Стефана – Больцмана выражена через универсальные константы:
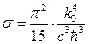. (1.22)
С помощью формулы (1.21) теоретически строго обосновывается закон смещения Вина, который обычно записывается для спектрального распределения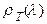 
по длинам волн 
.Примем во внимание соотношения
,
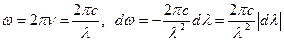тогда из равенства
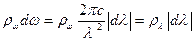
следует выражение для 
:
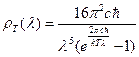. (1.23)
Исследуя (1.23) на экстремум, приходим к уравнению
5-y=5e-y , (1.24)
где 
. Это уравнение решается графически. Корень этого уравнения y*≈4,965 связывает температуру T и длину волны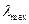 
, на которую приходиться максимальное значение 
:
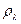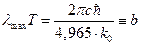. (1.25)
Это есть закон смещения Вина, где b называется постоянной Вина.
Итак, гипотеза Планка позволила разрешить «ультрафиолетовую катастрофу», обосновать законы равновесного излучения и вычислить значение введенной фундаментальной константы ћ - постоянной Планка.
Из соотношений (1.22) и (1.25) по экспериментальным значениям постоянных Стефана – Больцмана σ и Вина b, можно рассчитать постоянную ћ и уточнить значение постоянной Больцмана. Таким образом, впервые и было найдено значение ћ≈ 1,054∙10-34 Дж∙с и уточнено значение k0.
|
|
|
Из формулы Планка (1.21) видно, что при ћ→0 получается классическая формула Релея – Джинса. Уже и здесь проявилась фундаментальность этой физической константы, определяющей широкий круг физических явлений, для которых существенна дискретность величин.
|
|
|
