Определение состояния квантовой системы.

Второй, чрезвычайно важный, постулат касается математического определения состояния квантовой системы и его физического содержания. Классический способ определения состояния систем оказывается непригодным в квантовой области в силу корпускулярно-волнового дуализма. Согласно фундаментальной идее де Бройля состояние свободной частицы с определённым импульсом задаётся комплексной волновой функцией

, (5.1)

так называемой волной де Бройля. Функция (5.1), заданная во всём пространстве, математически представляет собой вектор бесконечномерного векторного линейного пространства.

Второй постулат можно рассматривать как математическое обобщение гениальной идеи де Бройля. Он утверждает: в квантовой механике состояние микрообъекта (любой системы) наиболее полно описывается вектором гильбертова пространства y. Причём y и сy (с –произвольное комплексное число) физически определяют одно и тоже состояние системы. Вследствие этого можно считать, что вектор состояния y удовлетворяет условию нормировки:

(y,y) = 1 (5.2)

Теоретически, смысл этого условия заключается в том, что состояние системы определяется лишь направлением вектора y.

 

Принцип суперпозиции состояний.

Квантовомеханический принцип суперпозиции утверждает: если квантовая система может находиться в состояниях, описываемых векторами гильбертова пространства y₁, y₂, …y_к, то она может находиться и в состоянии, описываемом линейной комбинацией этих векторов:

y = с₁y₁+с₂y₂+…+с_кy_к, (5.3)

где с₁, с₂ ,…, с_к, – произвольные комплексные числа, т.е. физически возможна суперпозиция состояний.

Важно обратить внимание на то, что состояние квантовой системы описывается вектором гильбертова пространства, норма которого равна 1, поэтому существенно только направление вектора. Отсюда следует, что векторы y и сy (с –произвольное комплексное число) описывают одно и то же состояние квантовой системы. В этом состоит особенность принципа суперпозиции квантовой механики, отличающая его от классического принципа суперпозиции. Отличие квантовой суперпозиции от классической можно проиллюстрировать таким примером. Суперпозиция двух классических волн приводит к возникновению новой волны, обладающей, естественно, и новыми физическими характеристиками. Квантовая же суперпозиция двух состояний, описывающихся одинаковыми векторами y₁ и y₂ = y₁, не приводит к новому состоянию в силу того, что вектор, описывающий получившееся состояние оказывается равным y = y₁+y₂ =2y₁, а, следовательно, направление векторов y и y₁ одинаково, т.е. они описывают одно и то же состояние.

Из принципа суперпозиции состояний следует, что все уравнения, которым удовлетворяют векторы состояний y, должны быть линейными (относительно y).

Принцип суперпозиции состояний отражает волновую природу микрочастиц и выполняется в нерелятивистской квантовой механике без исключения. Ярким подтверждением этого является опыт с интерференцией пучка электронов от двух щелей (§3, п.4). Сложение векторов состояний (волновых функций), а не вероятностей, представляет важнейшую особенность суперпозиции состояний в микромире.

Важным примером суперпозиции состояний, бесконечно мало отличающихся друг от друга (когда сумма (5.3) заменяется интегралом), является представление произвольного состояния микрообъекта суперпозицией волн де Бройля, т.е. состояний заданным импульсом частицы.[7]

 

Постулат квантования.

Четвёртый постулат – постулат квантования – утверждает: каждой физической величине А в квантовой механике сопоставляется линейный самосопряжённый (эрмитов) оператор Â, действующий в гильбертовом пространстве. Единственно возможным результатом измерений этой величины А являются собственные значения сопоставляемого ей оператора Â.

Линейность операторов физических величин обусловлена принципом суперпозиции. Эрмитовость же операторов обеспечивает вещественность предсказанных квантовой теорией результатов измерений физических величин, т.к. лишь у самосопряжённых операторов собственные значения вещественны (4.36): a_n = a_n*.

Спектр собственных значений эрмитова оператора Â, определяемый уравнением для собственных векторов и собственных значений (4.35), может быть дискретным, непрерывным или смешанным (§4, п.2). Случай дискретного спектра собственных значений оператора Â соответствует квантованию физической величины А:

Âj_n = a_nj_n, (5.4)

т.е. (a₁, a₂,…,a_n,…), чем и обусловлено название постулата. Согласно этому постулату, если вектор состояния y системы совпадает с одним из собственных векторов, j₁ например, оператора, то при измерениях физической величины получаются вполне определённые значения а_{1 .} Если же вектор состояния y не совпадает ни с одним из собственных векторов j_n оператора Â, то результат измерения физической величины А оказывается неоднозначным, т.е. при измерениях получаются различные значения, но всегда совпадающие с собственными значениями (a₁, a₂,…,a_n,…) оператора.

В случае непрерывного спектра собственных значений эрмитова оператора 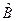, сопоставляемого физической величине В квантовой системы, при измерении будут получаться числа, совпадающие с собственными значениями b соответствующего оператора:

(5.4)

Это соответствует непрерывному изменению физической величины. Примером таких величин являются координаты, проекции импульсов и т.д.

 

Правила квантования.

Дла квантовомеханической системы результата измерения физической величины А, изображающейся эрмитовым оператором Â, в общем случае неоднозначен. Квантовая механика, как статистическая теория, должна предсказывать не только значения результатов измерения физической величины А, но и вероятности w_n возможных значений а_n этой величины в состоянии системы, которое описывается y вектором гильбертова пространства. Эти вероятности w_n и определяются пятым постулатом. Согласно четвертому: φ₁ а₁; φ₂ а₂, т.к. φ₁ и φ₂ – возможные состояния, тогда согласно третьему: Ψ = с₁φ₁ + с₂φ₂ – возможное состояние системы и вероятности w₁ = | с₁ | и w₂ = | с₂ | .

Пятый постулат – правила квантования – гласит: для системы, находящейся в состоянии Ψ, вероятность W_к получить при измерении физической величины А значение а_n равна квадрату модуля соответствующего коэффициента Фурье – разложения вектора Ψ по собственным векторам φ_n оператора Â, изображающего эту физическую величину:

W_n = | (φ_n, Ψ) | = | c_n | (5.5)

При непрерывном спектре собственных значений оператора Â квадрат модуля коэффициента Фурье–разложения | (φ_а, Ψ) | следует рассматривать как плотность вероятности.

В качестве примера рассмотрим результаты измерения величины А в состоянии квантовомеханической системы, когда Ψ = φ₁, где φ₁ – собственный вектор оператора Â, определяемый уравнением Âφ_n = а_nφ_n. В этом случае вероятность W₁ измерения значения а₁ равна 1, т.к. с₁ = (φ₁, φ₁) = 1, все же другие коэффициенты в разложении Ψ= с₁φ₁ + …с_nφ_n +…= равны нулю: (φ_n, φ₁) = 0 при n ≠ 1 в силу ортогональности собственных векторов эрмитовых операторов. Значит, полученные результаты можно записать в виде:

W_n =

Если же вектор состояния Ψ системы не совпадает ни с одним из собственных векторов φ_n оператора Â, то используя разложение Ψ в ряд Фурье по полной системе ортонормированных собственных векторов φ_n (4.42) и вычисляя коэффициенты с_n разложения по формуле (4.43), на основе четвертого постулата запишем:

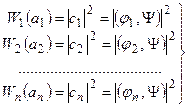, (5.7)

Очевидно, что

(5.8)

что легко доказать, учитывая, что норма вектора Y равна единице:

Из рассмотренных примеров следует, что пятый постулат, определяющий вероятности W_n измерения тех или иных дозволенных значений физической величины, вполне логично назвать правилами квантования.

 

⇐ Предыдущая3456789101112Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: