Существуют операторы, для которых справедливо равенство

 =  ⁺, (4.27)

они называются самосопряжёнными или эрмитовыми операторами. В квантовой механике в основном используются эрмитовы операторы. Условие самосопряжённости с учётом (4.24) записывается в виде:

(j,Ây) = (y,Âj)* (4.28)

Очевидно, что сумма самосопряжённых операторов есть самосопряжённый оператор. При умножении самосопряжённых операторов Â и Ĝ следует иметь в виду, что их произведение даёт эрмитов оператор лишь в том случае, если коммутатор их [Â,Ĝ] = 0, т.е. операторы–сомножители коммутируют друг с другом. Так как всякий оператор коммутирует сам с собой, то целая положительная степень эрмитова оператора Â есть так же эрмитов оператор:

Âⁿ = 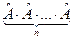(4.29)

Символом Î обозначается единичный оператор:

Îy = y (4.30)

Очевидно, ÎÂ = ÂÎ для любого оператора. Если для оператора Â можно подобрать такой коммутирующий с ним оператор Â^-1, что будет выполняться условие

 Â^-1 = Â^-1 = Î, (4.31)

то Â^-1 называется обратным по отношению к оператору Â.

Операторы, для которых

Â⁺ = Â^-1, (4.32)

называются унитарными операторами, следовательно, для них справедливо равенство:

Â⁺Â = Â^-1Â = Î. (4.33)

Легко доказать полезное соотношение:

. (4.34)

В) Собственные векторы и собственные значения самосопряжённыхоператоров.

Если в результате действия оператора Â на вектор j получается произведение некоторой константы a на тот же вектор, т.е выполняется равенство

Âj = аj, (4.35)

то вектор j называется собственным вектором оператора Â, принадлежащим его собственному значению а. Уравнение (4.35) называется уравнением для собственных векторов (функций) и собственных значений. Совокупность всех собственных значений называется спектром оператора. Спектр бывает дискретным, непрерывным или смешанным (дискретно-непрерывным).

Рассмотрим свойства собственных векторов и собственных значений эрмитовых операторов.

Теорема 1. Эрмитов оператор имеет вещественные собственные значения.

Доказательство. Итак, пусть дан эрмитов оператор Â, т.е. Â = Â⁺, и его уравнение для собственных векторов и собственных значений (дискретный спектр): Âj_n = а_nj_n. Требуется доказать, что a_n – действительные числа.

Пользуясь определением самосопряжённости оператора (4.28) для случая y = j = j_n, запишем:

(j_n,Âj_n) = (j_n,Âj_n) * = (Âj_n,j_n),

откуда

(j_n,a_nj_n) = (a_nj_n,j_n),

т.е a_n(j_n,j_n)=a_n*(j_n,j_n),

значит

a_n = a_n*,

т.е. собственные значения эрмитова оператора Â действительны.

Теорема 2. Собственные вектора j_n и j_m эрмитова оператора Â, принадлежащие различным собственным значениям a_n≠a_m, взаимно ортогональны.

Доказательство. На основе эрмитовости оператора (условие (4.28)) можно записать:

(j_m, Âj_n) = (Âj_m, j_n).

С учётом теоремы 1 и свойств скалярного произведения векторов (4.10) преобразуем это равенство к виду:

a_n (j_n, j_m)= a_m (j_m, j_n),

откуда

(a_n - a_m)(j_m, j_n)= 0.

Учитывая условие a_n≠a_m, получаем

(j_m, j_n)= 0, (4.37)

что означает ортогональность собственных векторов j_m и j_n, принадлежащих различным собственным значениям. Таким образом, теорема доказана.

Поскольку уравнение (4.35) однородно, то собственные вектора определяются им с точностью до произвольного множителя. Этот множитель можно выбрать так, чтобы норма собственных векторов, согласно (4.9), равнялась единице, т.е.

(j_n, j_n)= 1 (4.38)

Объединяя (4.37) и (4.38), получаем условие ортонормировки собственных векторов эрмитовых операторов с дискретным спектром:

(j_m, j_n) = δ_mn º (4.39)

Если спектр собственных значений оператора Â непрерывен, то собственные векторы нельзя пронумеровать числами. В этом случае собственные векторы зависят от собственных значений а как от параметра, что обозначается через j_а:

Âj_а = аj_а (4.40)

Так первая и вторая теоремы легко обобщаются и на случай непрерывного спектра собственных значений эрмитова оператора. Норма же собственных векторов в этом случае не является конечной, т.к. (j_а, j_а) = ∞. Поэтому условие ортонормировки записывается с помощью δ –функции Дирака:

(j_а,j_а) = δ(а΄-а) ≡ 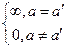(4.41)

В случае f –кратного вырождения некоторого собственного значения собственные векторы, принадлежащие ему, вообще говоря, не ортогональны. Однако, можно составить f линейных комбинаций из этих собственных векторов, удовлетворяющих условию ортонормировки. Система собственных векторов эрмитова[6] оператора является полной (замкнутой), если всякий вектор гильбертова пространства может быть разложен в ряд по собственным векторам эрмитова оператора, т.е

y = 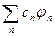(4.42)

Это выражение аналогично (4.5), когда базисными векторами являются собственные вектора j_n оператора Â. Для определения коэффициентов c_n в разложении (4.42) умножим его скалярно слева на j_m :

(j_m,y) = .

Тогда формула для коэффициентов разложения в (4.42) представиться в виде:

C_n = (j_n,y) (4.43)

В случае непрерывного спектра собственных значений оператора Â любой вектор y гильбертова пространства раскладывается в интеграл, подобный интегралу Фурье:

y = 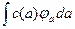, (4.44)

где j_a –собственный вектор оператора Â (4.40), коэффициенты разложения определяются формулой:

c(a) = (j_a,y) (4.45)

Действительно, достаточно (4.44) умножить слева скалярно на вектор j_a′, чтобы получить нужный результат:

(j_a′,y) = ∫(j_a′,c(a)j_a)da = ∫c(a)(j_a′,j_a)da = c(a′),

откуда следует формула (4.45).

Прямым следствием замкнутости (полноты) системы собственных векторов эрмитовых операторов является выражение скалярного произведения двух векторов гильбертова пространства:

(y, Ф) = ∫c*(a)b(a)da, (4.46)

где c(a) и b(a) – проекции векторов y и Ф на базисные векторы j_a, т.е. на собственные векторы эрмитова оператора Â.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: