 |
Интерференция электронов от двух щелей.
|
|
|
|
Объяснение интерференции света на основе волновых представлений было дано в начале ХIХ века Юнгом. Его знаменитый опыт заключался в следующем: монохроматический свет из точечного источника 1 (рис.1.7.) падает на экран с двумя малыми щелями А и В, попадая затем на экран-детектор 3, регистрирующий интенсивность падающего на него света.. Эта интенсивность на рис.1.7 представлена интерференционной кривой J(x), которая очень просто объясняется с волновой точки зрения о свете.
Если затем постепенно уменьшать интенсивность света от источника 1, освещенность экрана, естественно, уменьшается, однако, интерференционная картина сохраняется. Увеличивая время экспозиции, можно получить интерференционную кривую J(x) в принципе при сколь угодно малой интенсивности света. Но тогда с корпускулярной точки зрения о свете легко прийти к выводу: распределение попаданий отдельных фотонов дает на экране-детекторе ту же интерференционную картину J(x), как и световые
 |
волны.
Рис.1.7.
Нетрудно представить мысленный эксперимент, в котором интерференционная картина останется той же, но в точке 1 будет помещен источник монохроматических электронов, при этом опять можно уменьшать интенсивность электронного пучка настолько, что можно считать электроны, проходящими через прибор (интерферометр) поодиночке.
 |
С другой стороны, так как в природе никогда не наблюдалось половины или части электрона, то каждый электрон в этом опыте может пройти через одну из щелей: через щель А или через щель В. Значит, при закрытой щели В картина распределения электронов на экране, прошедших через щель А, представится пунктирной кривой
, а при закрытой щели А электроны, проходя через щель В, и попадая на экран, дают распределение интенсивности в согласии с пунктирной кривой 
(рис.1.8).|
|
|
Рис.1.8.
Поскольку интенсивность J(x) представляет распределение вероятности попадания электронов в различные точки экрана, то по теореме сложения вероятностей при открытых обеих щелях А и В распределение электронов на экране должно представляться суммой распределений для каждой из щелей в отдельности (сплошная кривая J(x)).
 |
Хотя логика этого эксперимента кажется безукоризненной, распределение, характерное для открытых обеих щелей А и В, не имеет места. Вместо этого, по убеждению физиков, должна наблюдаться стандартная интерференционная картина для двух щелей (рис.1.9), как и в случае со светом (фотонами). Этот эксперимент получил название «великого парадокса».
Рис.1.9.
 |
В 1961 году удалось зафиксировать на фотопластинке подлинную картину интерференции электронов на двух щелях в эксперименте, выполненном К.Иенссоном[5]. Интерференционная картина совпала с той, которую и ожидали физики, вопреки логике здравого смысла. Схема опытной установки Иенссона (в Тюбингенском университете), в принципе повторяет мысленный эксперимент, изображенный на рис.1.10.
Рис. 1.10.
Единственный способ объяснения этих парадоксальных результатов состоит в создании адекватного математического формализма, совместимого с идеей дискретности значений физических величин и всегда правильно предсказывающего наблюдаемые интерференционные явления. Но математический аппарат связан с интерпретацией волновой функции 
, описывающей состояние квантовой системы. Действительно, если учесть, что вероятность обнаружить частицу в точке с координатами x,y,z в момент времени t пропорциональна квадрату модуля волновой функции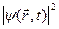 
, то отсюда следует, что волновую функцию целесообразно считать амплитудой вероятности. Тогда квадрат амплитуды вероятности равен плотности вероятности обнаружения частицы в момент t с координатами x,y,z:
|
|
|
.
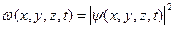Если событие может произойти несколькими взаимоисключающими способами (как, скажем, при прохождении электрона через одну из щелей А или В в рассматриваемых экспериментах), то амплитуда вероятности этого события представляет собою сумму амплитуд вероятностей каждого из способов:
(3.10)
Это утверждение совпадает с правилом сложения амплитуд в оптике. В рассмотренном выше примере функция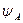 
представляет волну, проходящую через щель А, а 
– через щель В. На экране обе волны перекрываются и дают классическую интерференционную картину от двух щелей:
(3.11)
причем 
, т.е. последние два слагаемых в (3.11) и обеспечивают интерференционную картину.
Таким образом, главное, что следует из квантовой механики, можно сформулировать так:
1) основными закономерностями в природе являются закономерности не динамического, а статистического типа;
2) с вероятностями в природе следует обращаться не всегда так, как это принято в классических статистических теориях. Оказывается, что в определенных случаях необходимо складывать не сами вероятности событий, а амплитуды этих вероятностей, что и приводит к специфическим интерференционным эффектам.
Интересно в этом отношении высказывание М. Борна: «Статистические методы в физике по мере развития науки распространялись все больше и больше, и сегодня можно сказать, что современная физика полностью опирается на статистическую основу… Сегодня квантовая теория привела нас к более глубокому пониманию: она установила более тесную связь между статистикой и основами физики. Это является событием в истории человеческого мышления, значение которого выходит за пределы самой науки».
Более того, как отмечает Мякишев: «Главное отличие квантовой механики от классической заключается …в том, что в квантовой механике первичной величиной служит не вероятность, а ее амплитуда – волновая функция».
Глава II. Математический аппарат и аксиоматика квантовой механики.
§ 4. Математический аппарат квантовой механики.
При построении новой теории можно выделить три этапа: первый этап, на котором формируются и осмысливаются основополагающие идеи и закладывается физический фундамент теории; на втором этапе подбирается адекватный физическим идеям математический аппарат, позволяющий достаточно просто и логически стройно изложит соответствующую физическую теорию, т.е. производится "сшивание" физических идей и математического аппарата; на третьем этапе математический аппарат, нагруженный физическим содержанием, загружается в работу, получаемые при этом результаты сравниваются с экспериментальными данными, новые результаты проверяются на опыте. Вследствие этого продолжается осмысление физического содержания теории и развитие математического аппарата, что способствует расширению возможностей применения теории и более глубокому пониманию её идей.
|
|
|
Так, например, когда И.Ньютон создавал классическую механику, ему пришлось разрабатывать математический аппарат, который в дальнейшем послужил основанием для развития дифференциального и интегрального исчисления. В период же создания квантовой механики подходящий математический аппарат уже существовал как теория линейных операторов в линейном векторном пространстве
4.1. Векторы в линейном векторном пространстве.
А) Линейное векторное (комплексное) пространство.
Различные математические объекты, для которых определены операции сложения и умножения на число (комплексное в общем случае), называются векторами. Множество векторов образует линейное векторное (комплексное) пространство, если любая линейная комбинация векторов из этого множества есть вектор того же множества.
В квантовой механике вектор как элемент линейного векторного пространства обозначается символами ψ, φ, χ и т.д. Используются и другие обозначения, отражающие (или оставляющие без внимания) дискретный или непрерывный характер множества векторов: ψn и ψ, φn и φ, где n = 1,2,3,...
Для операций сложения векторов и умножения на число постулируются следующие свойства:
1. ψ1 + ψ 2 = ψ2 + ψ1;
2. (ψ1 + ψ 2) + ψ3 = ψ1 + (ψ2 + ψ3);
|
|
|
3. 1·ψ = ψ;
4. (c1 + c2)ψ = c1ψ + c2ψ, c1 и c2 – любые комплексные числа;
5. c1(c2ψ) = c1c2ψ; (4.1)
6. c(ψ1 + ψ2) = cψ1 + cψ2;
7. множество содержит нулевой вектор, такой, что ψ1 + 0 = ψ1;
8. ψ1 + (-ψ1) = 0.
Указанные действия с векторами справедливы, например, для обычных (геометрических) векторов, матриц, комплексных функций действительного переменного, т.е. волновых функций. Из вышеуказанных объектов можно построить линейные пространства, в которых линейные комбинации векторов в виде суммы
Ψ=Σcnφn (4.2)
|
|
|
