 |
3.11. Задачи динамики в сопротивлении материалов
|
|
|
|
Рис. 3. 23
Участок ВС:  .
.
N = –RВ = –0, 083 ql; Q = –Х1 + qz; М = Х1z –  ;
;
z = 0; Q = –Х1 = –0, 417ql; М = 0.
z = l ; Q = –0, 417ql + ql = 0, 583ql; М = 0, 417ql·l – 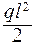 .
.
.
На участке ВС эпюра Q пересекает элемент (стержень) и меняет знак с (+) на (-), следовательно, на эпюре М в этом сечении – экстремум максимум.
Исследование на экстремум:
Q = 0; –Х1 + qz = 0;
z =  ;
;
 .
.
Выбираем масштаб и строим окончательные эпюры N, Q и M (см. рис. 3. 23).
3. 11. Задачи динамики в сопротивлении материалов
(к контрольной задаче № 11)
Пример № 19. На двух балках двутаврового сечения №16 (рис. 3. 24) установлен двигатель весом Q = 2, 1 т делающий n = 400 об/мин. Центробежная сила инерции, возникающая вследствие неуравновешенности вращающихся частей двигателя, равна H = 1, 1 т. Собственный вес балок и силы сопротивления можно не учитывать. Требуется найти: 1) частоту собственных колебаний  ; 2) частоту изменения возмущающей силы
; 2) частоту изменения возмущающей силы  ; 3) коэффициент нарастания колебаний
; 3) коэффициент нарастания колебаний 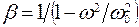 (если коэффициент
(если коэффициент 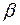 , определяемый по этой формуле, окажется отрицательным, то в дальнейшем расчете следует учитывать его абсолютную величину); 4) динамический коэффициент
, определяемый по этой формуле, окажется отрицательным, то в дальнейшем расчете следует учитывать его абсолютную величину); 4) динамический коэффициент  ; 5) наибольшее нормальное напряжение в балках
; 5) наибольшее нормальное напряжение в балках 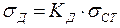 .
.
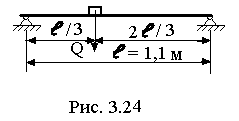 1. Определим частоту собственных колебаний
1. Определим частоту собственных колебаний  . Для упругих систем с одной степенью свободы без учета собственной массы
. Для упругих систем с одной степенью свободы без учета собственной массы  определяется формуле:
определяется формуле:  ,
,
где уСТ – перемещение точки приложения веса двигателя при статиче-
ском действии этого веса;
g – ускорение силы тяжести, 981 см/с2.
Определим уСТ, воспользовавшись методом сил.
Строим эпюру  (грузовую): Определим реакции опор (рис. 3. 25) от действия силы Q:
(грузовую): Определим реакции опор (рис. 3. 25) от действия силы Q: 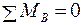 ;
;
|
|
|
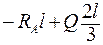 = 0,
= 0,
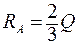 ,
,
 ;
; 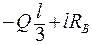 = 0,
= 0,
 .
.
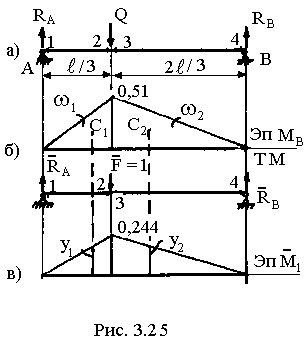 Применив метод характерных сечений 1, 2, 3, 4, получим:
Применив метод характерных сечений 1, 2, 3, 4, получим:
М1 = 0, М2 = М3 =
= 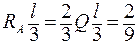 × 2, 1× 1, 1 = 0, 51 тм, М4 = 0.
× 2, 1× 1, 1 = 0, 51 тм, М4 = 0.
Строим грузовую эпюру.
Определим реакции опор от действия единичной силы 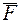 = 1.
= 1.
 ;
; 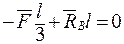 ;
;  .
.
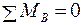 ;
; 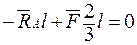 ;
; 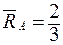 .
.
Строим эпюру 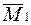 (единичную):
(единичную):
М1 = 0; М2 = М3 =  = 0, 244; М4 = 0. (рис. 3. 25, в) и вычислим статический прогиб, используя способ Верещагина:
= 0, 244; М4 = 0. (рис. 3. 25, в) и вычислим статический прогиб, используя способ Верещагина:
 ,
,
где 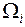 – площади составляющих грузовой эпюры;
– площади составляющих грузовой эпюры;
уi – ординаты единичной эпюры под центрами тяжести составляющих площадей грузовой эпюры;
Е = 2× 106 кГс/см2 – модуль Юнга;
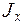 – осевой момент инерции сечения.
– осевой момент инерции сечения.
Для двух балок двутаврового сечения № 16 Jх = 2× 873 см4
(См. ПРИЛОЖЕНИЕ 1).
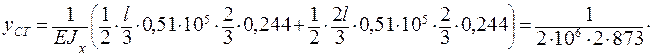
 = 0, 013 см.
= 0, 013 см.
тогда 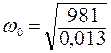 = 274 1/с.
= 274 1/с.
2. Определим частоту изменения возмущающей силы:
 = 41, 9 1/с.
= 41, 9 1/с.
3. Определим коэффициент нарастания колебаний:
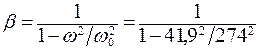 = 1, 024.
= 1, 024.
1. Определим динамический коэффициент
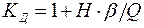 = 1+ 1, 1·1, 024/2, 1 = 1, 54.
= 1+ 1, 1·1, 024/2, 1 = 1, 54.
2. Определим наибольшее нормальное динамическое напряжение в балке

где 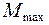 – максимальный изгибающий момент при действии силы Q
– максимальный изгибающий момент при действии силы Q
статически, т. е. 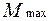 =
=  = 0, 51 тм (рис. 3. 25, б)
= 0, 51 тм (рис. 3. 25, б)
Wх – момент сопротивления сечения. Для двух балок двутаврового сечения №16 W = 2. 109 (см3) ( см. ПРИЛОЖЕНИЕ 1). Окончательно получим:
 = 360 кГс/см2 = 36 Мпа.
= 360 кГс/см2 = 36 Мпа.
3. 12. Расчет на прочность при переменных напряжениях
(к контрольной задаче № 12)
Теории прочности, разработанные и достаточно проверенные на опытах при постоянных напряжениях, непосредственно неприменимы к случаю переменных напряжений. В настоящее время этот вопрос еще недостаточно разрешен. Практически в расчетах при плоском напряженном состоянии, характеризуемом нормальным напряжением s и касательным напряжением t, для определения коэффициента запаса прочности используется следующая зависимость:
|
|
|
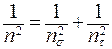 , (3. 43)
, (3. 43)
где n – искомый коэффициент запаса;
 ,
, 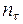 – коэффициенты запаса в предположении, что действует соответственно только нормальные напряжения
– коэффициенты запаса в предположении, что действует соответственно только нормальные напряжения  или только касательные напряжения
или только касательные напряжения  , которые определяются по формулам:
, которые определяются по формулам: 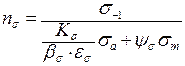 ,
,  , (3. 44)
, (3. 44)
где sа , sm – амплитудное и среднее напряжения рабочего цикла;  – предел выносливости материала при симметричном цикле изменения нормальных напряжений; ys – коэффициент влияния ассиметрии цикла; Ks – эффективный коэффициент концентрации напряжений; es – масштабный коэффициент; bs – коэффициент состояния поверхности.
– предел выносливости материала при симметричном цикле изменения нормальных напряжений; ys – коэффициент влияния ассиметрии цикла; Ks – эффективный коэффициент концентрации напряжений; es – масштабный коэффициент; bs – коэффициент состояния поверхности.
Аналогично для коэффициента по касательным напряжениям 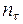 .
.
Из уравнения (3. 43) находится искомый коэффициент запаса
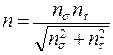 . (3. 45)
. (3. 45)
Пример № 20. В опасном сечении вала с диаметром d = 35 мм действует крутящий момент МK = 250 Нм и изгибающий момент Ми = 260 Нм. Вал сделан из углеродистой стали (предел прочности которой равен  = 550 МПа, а предел текучести
= 550 МПа, а предел текучести  = 260 МПа) и не имеет резких переходов, выточек, канавок; поверхность его чисто обработана резцом. Определить коэффициент запаса прочности в опасном сечении вала, приняв нормальные напряжения изгиба изменяющимися по симметричному циклу, а касательные напряжения кручения – по пульсирующему циклу.
= 260 МПа) и не имеет резких переходов, выточек, канавок; поверхность его чисто обработана резцом. Определить коэффициент запаса прочности в опасном сечении вала, приняв нормальные напряжения изгиба изменяющимися по симметричному циклу, а касательные напряжения кручения – по пульсирующему циклу.
Коэффициенты концентрации напряжений и масштабные коэффициенты можно считать одинаковыми для нормальных и для касательных напряжений. Решение: 1. Определим максимальные нормальные и максимальные касательные напряжения
 = 61, 8× 106 н/м2 = 61, 8 МПа.
= 61, 8× 106 н/м2 = 61, 8 МПа.
 = 29, 7× 106 н/м2 = 29, 7 МПа.
= 29, 7× 106 н/м2 = 29, 7 МПа.
2. По эмпирическим формулам [4] определим механические характеристики материала: предел текучести при кручении:
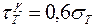 = 0, 6× 260 = 156 Мпа;
= 0, 6× 260 = 156 Мпа;
предел выносливости на кручение при симметричном цикле:
 = 0, 22× 550 = 121 Мпа;
= 0, 22× 550 = 121 Мпа;
предел выносливости на изгиб при симметричном цикле:
 = 0, 4× 550 = 220 Мпа.
= 0, 4× 550 = 220 Мпа.
3. Коэффициент концентрации напряжений определим по формуле:  = 1, 227.
= 1, 227.
4. Масштабный коэффициент определим по формуле:
 = 1, 2 + 0, 1 (3, 5 - 3) = 1, 25 где d – в см.
= 1, 2 + 0, 1 (3, 5 - 3) = 1, 25 где d – в см.
5. Коэффициент состояния поверхности берем (см. ПРИЛОЖЕНИЕ 5)
|
|
|
 = 0, 9.
= 0, 9.
6. Определим коэффициент запаса прочности по нормальным напряжениям по формуле (3. 44): 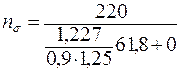 = 3, 26.
= 3, 26.
( 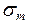 = 0,
= 0, 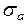 =
=  = 61, 8 МПа, так как имеем симметричный цикл)
= 61, 8 МПа, так как имеем симметричный цикл)
По касательным напряжениям  = 0; (см. ПРИЛОЖЕНИЕ 6).
= 0; (см. ПРИЛОЖЕНИЕ 6).
Так как касательные напряжения меняются по пульсирующему циклу, то  = 14, 85 МПа.
= 14, 85 МПа.
Тогда по формуле (3. 44):  = 7, 47.
= 7, 47.
Из (3. 45) получим  = 2, 97.
= 2, 97.
8. Коэффициенты запаса  и
и 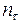 по отношению к пределу текучести равны
по отношению к пределу текучести равны 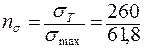 = 4, 21;
= 4, 21;  = 5, 25.
= 5, 25.
Общий коэффициент запаса прочности по текучести согласно (3. 45):
 = 3, 28.
= 3, 28.
Таким образом, принимаем коэффициент запаса по выносливости n = 2, 97, т. к. этот ниже коэффициента запаса по текучести.
|
|
|


