Между показателями надежности

Между основными показателями надежности существуют ана­литические зависимости. Приведем некоторые из них.

Зависимость между вероятностью безотказной работы и сред­ней наработкой до отказа определяется по выражению (1.13):

Так как f(t) = Q'(t) и Q(t) = 1 - P(t), то, выполнив интегрирова­ние по частям, получим

Учитывая, что

имеем

(4.1)

т. е. средняя наработка до отказа равна площади под кривой вероятности безотказной работы объекта.

Связь между вероятностью безотказной работы и интенсивностью отказов. Число объектов, которые будут исправно работать к моменту времени t, в среднем

где 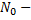число объектов, поставленных на испытания. К моменту их число составит

Тогда число отказавших объектов n (t) определяется как разность:

.

Подставив значения в выражение (1.18), получим

Устремив 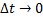и переходя к пределу, получим

(4.2)

После интегрирования (4.2) имеем

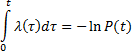
или

(4.3)

Связь между вероятностью безотказной работы, интенсивно­стью отказов и средней наработкой до отказа. Среднюю наработ­ку до отказа можно вычислить через интенсивность отказов. Под­ставив в выражение (4.1) значение (4.3), получаем

(4.4)

Для нормального периода эксплуатации поэтому

(4.5)

Таким образом, при постоянной интенсивности отказов объ­екта его средняя наработка до отказа есть величина, обратная ин­тенсивности отказов. В этом случае ВБР можно записать в виде

(4.6)

Плотность вероятности f(t) при этом связана с интенсивностью отказов следующим образом:

(4.7)

Зависимость между плотностью вероятности времени безот­казной работы и параметром потока отказов. Пусть в момент на испытании находится N _o объектов. По мере выхода из строя отказавшие объекты заменяются новыми (выборка с возмещени­ем), если объекты невосстанавливаемые. Тогда параметр потока отказов определяется по выражению (1.21). Среднее число от­казавших объектов в любой интервал времени от t до пропорционально значению ,длине интервала времени и числу испытуемых объектов N_o, т. е.

Число отказавших объектов можно представить в виде суммы

где n(t) — число отказавших объектов из числа тех объектов, ко­торые были поставлены на испытания первоначально; m(t) — чис­ло отказавших объектов из числа замененных в процессе испыта­ний за время от 0 до t,

Для определения m(t) выберем некоторый промежуток време­ни от τ до предшествующий t. В этот промежуток времени откажет объектов. Очевидно, что столько же объектов будет заменено новыми. Из этих замененных элементов на интер­вале времени от t до откажет объектов.

Для определения m(t) необходимо провести суммирование по всем интервалам времени, предшествующим t:

тогда

или

(4.8)

Полученное уравнение известно под названием уравнения Вольтерра. Решение уравнения демонстрирует (независимо от вида функции f(t), т. е. независимо от закона распределения времени безотказной работы), что параметр потока отказов объектов стре­мится к постоянной величине — обратной средней наработке на отказ, т. е. справедливо выражение

Связь между вероятностью восстановления и интенсивностью восстановления. Рассмотрим условную вероятность 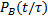того, что восстановление работоспособности объекта произойдет на ин­тервале времени t, следующем за интервалом τ после отказа, на котором еще не удалось восстановить работоспособность объекта

(4.9)

Предел отношения 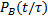при есть не что иное, как диф­ференциальная плотность вероятности восстановления в мо­мент τ при условии, что объект не был восстановлен до момента τ

(4.10)

Представляя (4.10) в виде

и учитывая, что Р_в(0) = 0, получаем аналогично формуле (4.3)

(4.11)

Средний ресурс, т.е. средняя наработка до предельного состоя­ния, характеризует долговечность ЭА, среднее время восстанов­ления — его ремонтоспособность.

4.3.

⇐ Предыдущая78910111213141516Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: