 |
Случайные величины, используемые
|
|
|
|
В ТЕОРИИ НАДЕЖНОСТИ
В теории надежности приходится иметь дело с двумя классами случайных величин — дискретными и непрерывными. Примеры дискретных случайных величин: число отказов или число восстановлений объекта за заданное время. Примеры непрерывных случайных величин: наработка объекта до отказа, наработка объекта между двумя отказами, время восстановления, ресурс. В соответствии с этим рассмотрим два класса распределений: дискретные и непрерывные.
Центральным понятием теории надежности является понятие «отказ», заключающееся в нарушении работоспособного состояния объекта. Хотя сам факт отказа объекта — явление детерминированное, но неполнота сведений об объекте и протекающих в нем и окружающей среде процессов приводят к вероятному характеру отказов, т. е. отказ объекта может быть вызван разными причинами и иметь различные особенности (см. раздел 1.3). Так как время появления отказа — величина случайная, вероятность этого события может быть вычислена с помощью разнообразных подходов. Наиболее обоснованным из них является применение в теории надежности методов теории вероятностей, математической статистики и теории случайных процессов. Поэтому здесь целесообразно повторить основные положения этих математических методов.
Нарушение условия функционирования ЭА является случайным событием, оно возникает как результат большого числа других событий в системе, и естественно, может произойти или нет. Событие, которое обязательно произойдет, называется достоверным, а которое не может произойти — невозможным.
При расчете надежности ЭА необходимо уметь интерпретировать комбинации событий.
|
|
|
Пусть А — некоторое событие. Противоположное ему событие обозначается  . События А и Вназываются несовместимыми, если наступление одного из них исключает появления другого, т. е.
. События А и Вназываются несовместимыми, если наступление одного из них исключает появления другого, т. е. 
Если два независимых события А и Ввозникают одновременно, т. е. появление одного из них непременно будет вызывать появление другого, то их называют совместными 
Допустим, что из п испытуемых аппаратов только m благоприятствуют событию А. Отношение 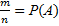 называется вероятностью события А. P(A) — безразмерная величина, она служит «мерой случайности» событий и обладает следующими свойствами:
называется вероятностью события А. P(A) — безразмерная величина, она служит «мерой случайности» событий и обладает следующими свойствами:
1) если А — достоверное событие, то Р(А) = 1;
2) если А — невозможное событие, то Р(А) = 0;
3) если А и В являются несовместимыми событиями, то Р(А + В) = Р(А) + Р(В) или Р(АВ) = 0;
4) если А и B — совместные события, то Р(АВ) = Р(А)Р(В);
5) если А и  , то Р(А) = 1-Р(
, то Р(А) = 1-Р( ).
).
Вероятность совместного появления двух событий А и В равна вероятности одного из них, умноженной на условную вероятность другого, вычисленную в предположении, что первое событие наступило. Примером наступления взаимосвязанных и совместных событий можно назвать возникновение большой зоны выброса ионизированных газов из ЭА, что приводит к образованию электрической дуги между линиями силовой цепи.
К случайным событиям, характеризующим надежность ЭА, следует отнести: отказ работоспособности; полный отказ работоспособности; ложное срабатывание; резервирование и т. д.
Отказ работоспособности — событие, заключающееся в переходе объекта с одного уровня работоспособности на другой, более низкий. Уровень работоспособности определяется заданными перечнем и объемом функции, который ЭА способен выполнять.
Полный отказ работоспособности — неработоспособное состояние.
Ложное срабатывание — срабатывание аппарата при отсутствии требования срабатывания данного и других изделий системы.
Резервирование — наличие резервных элементов, которые включаются только после автоматического отключения отказавших элементов. Так продлевается работоспособность системы.
|
|
|
Количественной оценкой случайного события является случайная величина, принимающая в результате опыта то или иное значение. Между случайной величиной и случайным событием существует тесная связь. За случайную величину можно принять число однородных случайных событий за определенный промежуток времени. Случайные величины имеют численное значение и подчиняются тем или иным объективным закономерностям. Основой для их изучения является статистический материал и методы теории вероятностей.
К случайным величинам в аппаратостроении относятся: наработка до отказа, время отказной работы, износостойкость и т. д.
Случайной величиной на вероятном пространстве  называется измеримая функция,
называется измеримая функция,  определенная на Ω, т. е. некоторая функция элементарного события
определенная на Ω, т. е. некоторая функция элементарного события  .
.
Вероятностным пространством (полем вероятностей)  называется совокупность трех объектов — пространства элементарных событий Ω, σ-алгебры событий и вероятной меры Р(А).
называется совокупность трех объектов — пространства элементарных событий Ω, σ-алгебры событий и вероятной меры Р(А).
Пространство элементарных событий Ω — произвольное множество, элементы которого (элементарные события) будем обозначать буквой ω. Событие Е называется элементарным, если для всякого события А случайного эксперимента оно влечет либо А, либо  . Непустое множество событий, которое удовлетворяет условиям:
. Непустое множество событий, которое удовлетворяет условиям:
1) если 
2) если 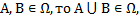
называется алгеброй событий.
Если алгебра событий такова, что с каждой бесконечной последовательностью событий 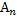 она содержит и сумму событий
она содержит и сумму событий  и произведение событий
и произведение событий  то такая алгебра называется σ-алгеброй. Событие
то такая алгебра называется σ-алгеброй. Событие  , состоит в том, что из последовательности событий
, состоит в том, что из последовательности событий 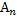 , происходит, по крайней мере, одно, а событие
, происходит, по крайней мере, одно, а событие  — в том, что происходят все события
— в том, что происходят все события 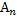 одновременно. Мерой на σ-алгебре подмножеств ψназывается неотрицательная счетно-аддитивная функция Р(А) множества, т. е. такая функция, для которой
одновременно. Мерой на σ-алгебре подмножеств ψназывается неотрицательная счетно-аддитивная функция Р(А) множества, т. е. такая функция, для которой
 (4.12)
(4.12)
для всякой последовательности попарно непересекающихся множеств  из ψ Другими словами, числовая функция
из ψ Другими словами, числовая функция  определенная на ψи обладающая свойствами (1.1) и
определенная на ψи обладающая свойствами (1.1) и  для произвольной последовательности попарно несовместимых событий
для произвольной последовательности попарно несовместимых событий  1, 2,... (
1, 2,... (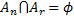 при
при  ), называется вероятностью. Следовательно, функция
), называется вероятностью. Следовательно, функция  является мерой, заданной на ψи удовлетворяющей условию нормировки
является мерой, заданной на ψи удовлетворяющей условию нормировки  (вероятностной мерой). Пара объектов — некоторое множество Ω и некоторая σ-алгебра его подмножеств ψ — называется измеримым пространством
(вероятностной мерой). Пара объектов — некоторое множество Ω и некоторая σ-алгебра его подмножеств ψ — называется измеримым пространством  Таким образом, вероятностное пространство — это измеримое пространство с нормированной мерой на нем. Случайная величина полностью определена, если известен исход эксперимента ω. Обычно случайные величины обозначают ξ вместо ξ(ω), не указывая на зависимость от элементарного события.
Таким образом, вероятностное пространство — это измеримое пространство с нормированной мерой на нем. Случайная величина полностью определена, если известен исход эксперимента ω. Обычно случайные величины обозначают ξ вместо ξ(ω), не указывая на зависимость от элементарного события.
|
|
|
Исчерпывающей характеристикой случайной величины является ее функция распределения. Для задания распределения величины достаточно задать функцию
 (4.13)
(4.13)
которая называется функцией распределения величины и является одномерной функцией распределения. Иначе  интегральным законом распределения. Если — дискретная величина, для которой
интегральным законом распределения. Если — дискретная величина, для которой  то
то

где  , если х > 0;
, если х > 0;  , если х < 0. Говорят, что ξ, имеет непрерывное распределение, если
, если х < 0. Говорят, что ξ, имеет непрерывное распределение, если  — непрерывная функция. Величина ξ, имеет непрерывное распределение, если существует такая функция
— непрерывная функция. Величина ξ, имеет непрерывное распределение, если существует такая функция  , что
, что
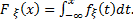 (4.14)
(4.14)
Функция  , удовлетворяющая соотношению (4.14), называется плотностью распределения величины ξ. Плотность
, удовлетворяющая соотношению (4.14), называется плотностью распределения величины ξ. Плотность  удовлетворяет следующим очевидным условиям:
удовлетворяет следующим очевидным условиям:
 (4.15)
(4.15)
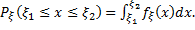 (4.16)
(4.16)
В частности, интенсивность отказов ЭА λ(t) в течение эксплуатации является плотностью распределения вероятностей. Тогда среднее время безотказной работы (средняя наработка до отказа) 
Пользуясь понятием функции распределения и плотности вероятности, можно дать определение непрерывной случайной величины.
Случайная величина называется непрерывной, если ее функция распределения непрерывна на всей числовой оси, а плотность распределения существует и непрерывна всюду.
Для дискретной случайной величины закон распределения удобно записывать в виде таблицы
| Случайные величины | 
| 
| — | 
| — |
| Вероятности | 
| 
| — | 
| — |
Иногда удобно изображать закон распределения графически. На дискретной системе координат по оси абсцисс откладываем значения случайной величины, по оси ординат — соответствующее ей значение вероятности. Соединяя точки, получаем ломаную кривую, которая называется многоугольником распределения.
|
|
|
 Пример 1. Проводятся испытания 6 контакторов на коммутационную износостойкость. Вероятность отказа каждого контактора равновелика. Тогда закон распределения имеет вид
Пример 1. Проводятся испытания 6 контакторов на коммутационную износостойкость. Вероятность отказа каждого контактора равновелика. Тогда закон распределения имеет вид

| ||||||

| 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
Графически закон распределения примет вид многоугольника (рис. 4.4).
 Пример 2. Проводится испытание контактора постоянного тока на 150 А типа КМ2000. Коммутационная износостойкость главных контактов контактора должна быть не менее 100 000 операций вероятности отказа. Вероятность отказа через каждые 20 000 операций равна
Пример 2. Проводится испытание контактора постоянного тока на 150 А типа КМ2000. Коммутационная износостойкость главных контактов контактора должна быть не менее 100 000 операций вероятности отказа. Вероятность отказа через каждые 20 000 операций равна

| ||||

| 0,2 | 0,4 | 0,6 | 0,8 |

Здесь х 1= 1 — после 20 000; х 2 = 2 — после 40 000;  — позиция после каждой 20 000 и т. д.
— позиция после каждой 20 000 и т. д.
Закон распределения имеет вид (рис. 4.5).
После 100 000 операций вероятности отказа считается, что происходит полный износ главных контактов, и контактор отключается.
Математическое ожидание случайной величины ξ (обозначается Мξ)есть предел
 (4.17)
(4.17)
где  — последовательность дискретных случайных величин, определяемых равенством ξ = k/n если
— последовательность дискретных случайных величин, определяемых равенством ξ = k/n если  Очевидно, что
Очевидно, что 
Математическое ожидание удовлетворяет следующим свойствам:
1) 
2) 
3) 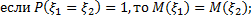
4) 
5) 
Для вычисления математического ожидания используются следующие формулы
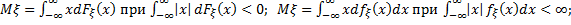 (4.18)
(4.18)
при условии, что интеграл справа существует.
Моменты случайных величин служат для описания свойств плотности распределения случайной величины ξ. Они содержат меньше информации о случайной величине по сравнению с плотностью распределения, но часто более удобны при решении прикладных задач. Величина
 (4.19)
(4.19)
называется k-м моментом величины ξ (если указанное математическое ожидание существует).
Часто величина  называется начальным моментом k- гопорядка случайной величины ξ. При k = 1 начальный момент первого порядка
называется начальным моментом k- гопорядка случайной величины ξ. При k = 1 начальный момент первого порядка  является математическим ожиданием непрерывной случайной величины ξ,
является математическим ожиданием непрерывной случайной величины ξ,
 (4.20)
(4.20)
Математическое ожидание  может быть оценено как статистическое среднее по
может быть оценено как статистическое среднее по  ,
,
i =  реализациям:
реализациям:
 (4.21)
(4.21)
причем  ; k-й момент центрированной случайной величины
; k-й момент центрированной случайной величины  ξ
ξ  называется k-м центральным моментом
называется k-м центральным моментом
 (4.22)
(4.22)
Особую роль играет второй центральный момент  , который называется дисперсией случайной величины ξ:
, который называется дисперсией случайной величины ξ:

Для не прерывных случайных величин
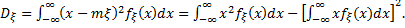 (4.23)
(4.23)
Статистически дисперсия по  реализациям рассчитывается по формуле
реализациям рассчитывается по формуле
 (4.24)
(4.24)
причем 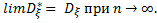
ДисперсР1я характеризует рассеивание значений случайной величины ξ, в окрестности ее математического ожидания. Наряду с дисперсией  , в качестве меры рассеивания широко используется среднее квадратическое отклонение случайной величины ξ (СКО)
, в качестве меры рассеивания широко используется среднее квадратическое отклонение случайной величины ξ (СКО)
|
|
|

Отметим два обстоятельства:
1)  всегда определена, если определено M ξ;
всегда определена, если определено M ξ;
2) если  , т. е. в этом случае величина ξ, с вероятностью 1 постоянна.
, т. е. в этом случае величина ξ, с вероятностью 1 постоянна.
В дальнейшем для сокращения записи будем обозначать начальные и центральные моменты случайной величины ξ, соответственно  и
и  . Начальный и центральный моменты нулевого порядка
. Начальный и центральный моменты нулевого порядка  .
.
Центральный момент третьего порядка
 (4.25)
(4.25)
характеризует асимметрию кривой плотности распределения  . Если
. Если  — симметричная непрерывная функция с осью симметрии, проходящей через
— симметричная непрерывная функция с осью симметрии, проходящей через  , то
, то  . В этом случае также равны нулю и все другие нечетные центральные моменты случайной величины ξ.
. В этом случае также равны нулю и все другие нечетные центральные моменты случайной величины ξ.
Центральный момент четвертого порядка
 (4.26)
(4.26)
характеризует эксцесс кривой плотности распределения  .
.
Если случайная величина ξ, непрерывна, то значения х, где плотность  достигает максимального значения, называются модами. Если мода единственна, то распределение случайной величины называют унимодальным, в противоположном случае — мультимодальным. Если ξ, — дискретная случайная величина и
достигает максимального значения, называются модами. Если мода единственна, то распределение случайной величины называют унимодальным, в противоположном случае — мультимодальным. Если ξ, — дискретная случайная величина и 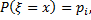 то ее модами называют те значения
то ее модами называют те значения  для которых
для которых
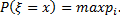 (4.27)
(4.27)
Медианой случайной величины ξ называется значение х', для которого
 (4.28)
(4.28)
Для случайных величин с непрерывным распределением медиана определяется как значение х', для которого
 (4.29)
(4.29)
Квантиль порядка  есть значение ха, для которого
есть значение ха, для которого
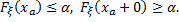 (4.30)
(4.30)
Если ξ, — случайная величина с непрерывным распределением, то квантиль ха порядка а определяется равенством  . Медиана является квантилью порядка 0,5.
. Медиана является квантилью порядка 0,5.
Условной вероятностью события А относительно события В, для которого Р(В) > 0, называется величина
 (4.31)
(4.31)
Формула умножения вероятностей:
 (4.32)
(4.32)
Общая формула умножения вероятностей:
 (4.33)
(4.33)
Формула полной вероятности. Пусть Е1, Е2,..., Еп — полная группа событий (предполагаем, что  ). Тогда для всякого события А
). Тогда для всякого события А

Формула Байеса дает выражение для условных вероятностей одного из событий Ек полной группы Е1, Е2,..., Еп при условии, что произошло событие А:
 (4.34)
(4.34)
Предположим, что событие А может происходить при гипотезе  , заключающейся в том, что произошло событие Ек с вероятностью Р(А/Ек), а Р(Ек)— вероятность гипотезы
, заключающейся в том, что произошло событие Ек с вероятностью Р(А/Ек), а Р(Ек)— вероятность гипотезы  .
.
Формула Байеса позволяет вычислить условную вероятность гипотезы Нк при условии, что произошло событие А, через вероятности гипотез и вероятности события А при различных гипотезах. Выражение
 (4.35)
(4.35)
называется условной функцией распределения величины ξ относительно события А. Она определена, если Р(А) > 0.
Если  непрерывна и
непрерывна и

то 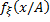 называется условной плотностью распределения величины ξ относительно события А. Условная функция распределения и условная плотность распределения обладают свойствами функции распределения и плотности распределения соответственно. Моменты, вычисленные по условной функции распределения, называются условными моментами случайной величины с,. В частности, выражение
называется условной плотностью распределения величины ξ относительно события А. Условная функция распределения и условная плотность распределения обладают свойствами функции распределения и плотности распределения соответственно. Моменты, вычисленные по условной функции распределения, называются условными моментами случайной величины с,. В частности, выражение
 (4.36)
(4.36)
если интеграл справа абсолютно сходится, называется условным математическим ожиданием величины £, относительно события А.
Формула полного математического ожидания имеет вид
 (4.37)
(4.37)
где Е1, Е2,..., Еп — полная группа событий;  .
.
С помощью условных функций и плотности распределения можно установить стохастическую зависимость между составляющими случайного вектора  .
.
Если вектор  ., состоит из т независимых составляющих
., состоит из т независимых составляющих  произведению плотностей распределения его составляющих:
произведению плотностей распределения его составляющих:
 (4.38)
(4.38)
Используя формулы (4.32) и (4.38), нетрудно показать, что из независимости случайных величин следует их некоррелированность. Обратное утверждение в общем случае неверно. Иначе говоря, условие независимости случайных величин более сильное, чем условие некоррелированности.
Производящие функции. Пусть v — целочисленная неотрицательная случайная величина с распределением вероятностей
 (4.39)
(4.39)
Производящей функцией распределения (4.39) случайной величины v называется ряд
 (4.40)
(4.40)
Для группы п целочисленных неотрицательных величин  совместная производящая функция определяется рядом
совместная производящая функция определяется рядом

где

Распределение вероятностей (4.39) однозначно определяется своей производящей функцией
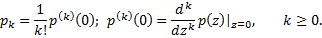
Математическое ожидание Mv выражается формулой

Факториальные моменты случайной величины  вычисляются по формуле
вычисляются по формуле

В частности, математическое ожидание M v и дисперсия D v определяются формулами
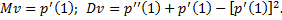
Преобразованием Лапласа p (s) неотрицательной случайной величины ξ с функцией распределения вероятностей 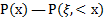 называется функция
называется функция
 (4.41)
(4.41)
Если распределение Р (х)имеет плотность и (х) = Р' (х),то преобразование Лапласа:
 (4.42)
(4.42)
Преобразование Лапласа можно представить в виде ряда
 (4.43)
(4.43)
в любом интервале  , в котором ряд сходится.
, в котором ряд сходится.
Преобразование Лапласа  при вещественных λ > 0 имеет вероятностный смысл
при вещественных λ > 0 имеет вероятностный смысл
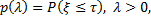 (4.44)
(4.44)
где τ — случайная величина, не зависящая от ξ и имеющая показательное распределение с параметром λ:
 (4.45)
(4.45)
при этом

Выражение (4.44) интерпретируется следующим образом:

При λ > 0 есть вероятность того, что интересующий нас момент (отказа, восстановления и т. д.) ξ, происходит до момента остановки наблюдений τ, имеющего показательное распределение.
Преобразование Лапласа  суммы
суммы  двух независимых случайных величин равно произведению преобразований Лапласа слагаемых
двух независимых случайных величин равно произведению преобразований Лапласа слагаемых

что равносильно равенству

Преобразование Лапласа  суммы
суммы

независимых между собой и от v одинаково распределенных случайных величин 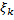 с преобразованием Лапласа
с преобразованием Лапласа  определяется суперпозицией функций ϕ(z) и
определяется суперпозицией функций ϕ(z) и 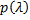 :
:
 (4.46)
(4.46)
где v — целочисленная неотрицательная случайная величина с производящей функцией 
Понятие преобразования Лапласа естественным образом распространяется на многомерные распределения.
4.4.
|
|
|


