 |
Число верных знаков приближенного числа
|
|
|
|
ЧИСЛЕННЫЕ МЕТОДЫ,
Ч. 1
УЧЕБНОЕ ПОСОБИЕ
МОСКВА 2005
ББК 22.193
К90
УДК 519.6
Рецензенты:
Шананин Н.А., к.ф.-м.н., доцент РУДН
Зильберглейт Л.В., к.ф.-м.н., доцент МИКХиС
К90 Куликов С.П., Самохин А.Б., Чердынцев В.В. Численные методы, ч. 1: Учебное пособие / Московский государственный институт радиотехники, электроники и автоматики (технический университет) – М., 2005. – с.
ISBN 5-7339-0211-6
Рассмотрены численные методы решения прикладных математических задач. Учебное пособие написано для студентов, обучающихся по математическим специальностям факультета кибернетики. Оно может быть полезным также при изучении дисциплин “Математическое моделирование” и “Методы оптимизации”.
Табл.3, Ил.60, Библиогр.: 4 назв.
Печатается по решению редакционно-издательского совета Московского государственного института радиотехники, электроники и автоматики (технического университета).
Без объявл. ББК 32.849+32.973-04
ISBN 5-7339-0211-6
© С.П. Куликов,
А.Б. Самохин,
В.В. Чердынцев.
Введение
Пятидесятилетняя эволюция ЭВМ от первых ламповых до современных серийных с быстродействием порядка 
операций в секунду привела к развитию математического моделирования и численного анализа практически во всех отраслях человеческого знания. Развитие технических возможностей, математического и программного обеспечения ЭВМ показали несовершенство некоторых классических методов решения инженерных и научно-технических задач, что обусловило развитие новых методов их численного решения. Проблема выбора оптимального численного метода решения как с точки зрения экономии ресурсов ЭВМ, так и снижения результирующей погрешности требует определенного опыта и вычислительной практики.
|
|
|
Настоящее пособие является введением в численные методы. В конце каждой темы приведены задания для практических занятий, выполнение которых позволяет глубже понять и усвоить вычислительные алгоритмы. При их решении допустимо использование инженерных калькуляторов и применение математических пакетов прикладных программ.
Абсолютная и относительная погрешности.
Численные методы служат для нахождения приближенного решения математических задач. Любое приближенное решение связано с ошибкой (погрешностью). Виды ошибок:
1. Погрешность математической модели, связанная с неполными знаниями о процессе.
2. Погрешность упрощения модели.
3. Погрешность, связанная с приближенным характером начальных данных.
4. Погрешность округления при расчетах.
Первые две погрешности относятся к систематическим, а две последние - к статистическим ошибкам. Для их оценки вводится абсолютная и относительная погрешности.
Абсолютная (предельная) погрешность – определяет интервал, в котором лежит точное значение величины.
Пусть А - точное значение величины (неизвестно), а а - приближенное значение величины (известно). За абсолютную погрешность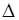 
принимается минимальное число 
, 
удовлетворяющее условию:
(1.1)
При статистических измерениях погрешность задается с определенной достоверностью, т.е. вероятность события 
больше определенной величины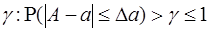 
. Перепишем определение: 
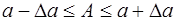, то есть точное значение 
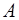лежит в заданном интервале. Для оценки качества измерений вводится относительная погрешность:
. (1.2)
Заданные величины или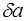 
позволяют записать точное значение А в символическом виде: 
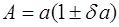или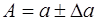 
.
Число верных знаков приближенного числа
Приближенное число можно представить в виде:
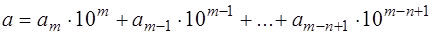, (1.1.1)
где m - величина старшего разряда, n - текущий номер знака, отсчитываемый слева направо. Говорят, что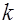 
первых знаков приближенного числа верные, если абсолютная погрешность удовлетворяют условию: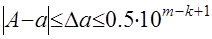 
, то есть меньше половины соответствующего разряда. Подбирается минимальное число вида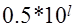 
большее, чем и сравниваются разряды.
|
|
|
Погрешность функций
Пусть дана функция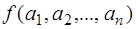 
от n приближенных значений 
, погрешности которых известны. Требуется определить погрешность функции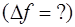 
.
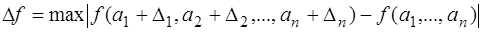, где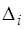 
- абсолютная погрешность приближенной величины . Если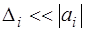 
, то разность, стоящую в формуле можно оценить в линейном приближении:
Отсюда следует оценка погрешности:
, 
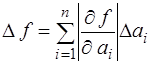(1.2.1)
|
|
|
