 |
Метод парабол. (Метод Симпсона)
|
|
|
|
Степень полинома n равна двум. 
Рассмотрим интервал длиной 2h: 
. Коэффициенты Котеса (4.1.1)равны:
, 
, 
.
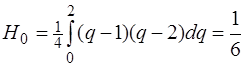В результате квадратурная формула имеет вид: 
.
Для применения метода парабол на [ a, b ],его необходимо разбить на 2n интервала, т.е. число интервалов должно быть четно. При суммировании по частичным интервалам внутренние четные точки удваиваются, В результате окончательная формула имеет вид:
, (4.4.1)
где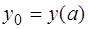 
, 
.
Оценка метода парабол: продифференцировав три раза выражение 
и применяя теорему о среднем, также как и в методе трапеций, получим:
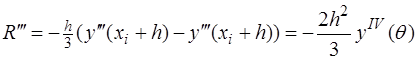, где 
.
Погрешность R зависит не от третьей, а от четвертой производной, т.е. приближение имеет повышенную точность и формула парабол верна для полиномов третьей степени. Окончательно, погрешность имеет вид:
, 
.
На практике, достижение заданной точности определяется путем сравнения значений интеграла, рассчитанных для текущего и удвоенного числа разбиений интервала.
Квадратурные формулы Гаусса
Предварительно необходимо рассмотреть свойства полиномов Лежандра: 
- полином степени n, 
. Полиномы ортогональны, то есть: 
, где 
- символ Кронекера.
Имеют n корней на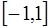 
. Для любого полинома 
: 
, если k < n,
так как полином степени k представим в виде линейной комбинации полиномов Лежандра до степени k включительно.
Исходим из формулы общего вида:
Для произвольного отрезка 
замена переменных 
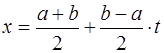переводит его в отрезок 
, и квадратурная формула Гаусса имеет вид:
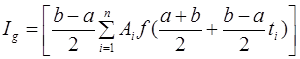(4.5.1)
Потребуем, чтобы квадратурная формула была точна для полиномов максимальной степени 
, а, следовательно, должна быть точна для 1, t, …, t 
. Система уравнений: 
нелинейная.
Используем свойство полинома Лежандра: 
при k =0,1, …, n -1.
Равенство интеграла нулю возможно, если 
- корни полинома Лежандра, которые известны.
|
|
|
Полученные , подставляются в первые n уравнений системы для определения коэффициентов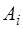 
:
, 
.
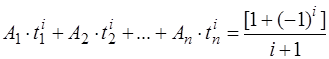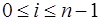Определитель системы – определитель Вандермонда ¹ 0 и система имеет единственное решение.
Оценка точности квадратурной формулы Гаусса проводится по формуле:
, где 
.
Задание для практических занятий
В практической работе исследуется сходимость различных методов в зависимости от 
- числа точек разбиения.
Рассматривается интеграл вида 
, где 
, значения K, L даны в табл. 4.3, 
.
Точное значение интеграла равно:
.
Сравнить его со значениями, полученными методом трапеций (4.3.1), методом парабол (4.5.1), методом Гаусса (4.7.1), коэффициенты этого метода приведены в табл. 4.1
Таблица 4.1
| i | ti | Ai | |
| n =4 | 1,4 |  0,861136
| 0,347854 |
| 2,3 | 0,339981
| 0,652145 | |
| n =6 | 1,6 | 0,932464
| 0,171324 |
| 2,5 | 0,661209
| 0,360761 | |
| 3,4 | 0,238619
| 0,467913 | |
| n =8 | 1,8 | 0,960289
| 0,101228 |
| 2,7 | 0,796666
| 0,222381 | |
| 3,6 | 0,525532
| 0,313706 | |
| 4,5 | 0,183434
| 0,362683 |
Результаты расчетов свести в табл. 4.2:
Таблица 4.2
| n | |||
| Itr | … | … | … |
| Ipar | … | … | … |
| Ig | … | … | … |
Построить график зависимости величины интегралов от n, на который нанести результаты расчетов и точное значение интеграла. Оценить качественно скорость сходимости различных методов.
Таблица 4.3
| № | ||||||||
| K | 3,2 | 3,4 | 3,6 | 3,8 | 4,0 | 2,2 | 2,4 | 2,6 |
| L | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 1,2 | 1,4 | 1,6 |
| № | ||||||||
| K | 2,8 | 3,0 | 1,2 | 1,4 | 1,6 | 1,8 | 4,2 | 4,4 |
| L | 1,8 | 2,2 | 0,8 | 1,0 | 1,2 | 1,4 | 3,2 | 3,4 |
Численные методы линейной алгебры
Рассматриваются численные методы решения систем линейных алгебраических уравнений (СЛАУ), а также нахождения собственных значений и собственных векторов матриц.
Численное решение СЛАУ
СЛАУ используются во многих областях науки и техники и являются наиболее часто встречающимся типом задач вычислительной математики. В общем виде СЛАУ из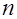 
уравнений с 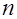неизвестными записывается в виде:
|
|
|
(5.1)
Здесь 
- неизвестный вектор решения, 
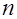- заданный вектор в -мерном пространстве, а
-
линейный оператор в этом пространстве, заданная матрица размером 
или в другом виде 
, 
Доказывается, что если определитель матрицы не равен нулю, то СЛАУ имеет единственное решение. Ниже будем полагать, что это условие выполняется. Однако, отличие определителя 
от нуля не могут служить гарантией того, что решение СЛАУ будет найдено численно с заданной точностью. Причиной этого может быть как плохая обусловленность самой системы, так и выбранного алгоритма. Заметим, что близость определителя к нулю и даже весьма малое его значение не свидетельствуют, вообще говоря, о плохой обусловленности системы. В качестве примера можно привести матрицу системы, у которой присутствует только главная диагональ с весьма малыми, но отличными от нуля коэффициентами. Определитель такой матрицы может быть машинный нуль, в тоже время свойства такой матрицы близки к единичной, а ошибка в решении порядка ошибки в задании исходных данных.
Для, так называемых, плохо обусловленных задач их решение принципиально нельзя получить совершенно точно. Для них малые изменения в исходных данных (коэффициентах матрицы и в векторе правой части), которые могут находиться в пределах точности их задания, приводят к несоразмерно большим изменениям в решении. В результате, в пределах точности задания исходных данных (например, в пределах ошибки округления из-за ограниченного формата числовых данных ЭВМ) может существовать множество различных решений, удовлетворяющих системе.
В качестве примера плохо обусловленной системы можно привести СЛАУ с почти линейно зависимыми строками (столбцами) в матрице. Плохо обусловленным алгоритмом для решения СЛАУ можно назвать метод Гаусса без выбора главного элемента.
Для характеристики обусловленности задачи вводят, так называемое, число обусловленности 
. Для задачи решения СЛАУ в качестве числа обусловленности можно принять
.
Здесь 
- какая-либо норма в пространстве 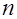-мерных векторов, которая выражается через норму вектора следующим образом:
|
|
|
Норма матрицы характеризует максимально возможное относительное увеличение по норме ненулевого вектора при воздействии на него матрицы.
Пусть решение СЛАУ получено с относительной ошибкой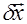 
. Тогда для нее справедлива оценка:
Здесь 
- машинная константа – наименьшее число, которое при прибавлении к единице ещё изменяет её значение в машинном представлении. Отметим, что оценка справедлива для малых ошибок в заданной матрице 
Введём понятие невязки 
решения:
(5.2)
Заметим, что малость невязки 
не гарантирует малость ошибки 
в решении. Так, для невязки выполняется соотношение 
,
в то время как для справедливо: 
Норма обратной матрицы для плохо обусловленной СЛАУ велика, также как и число обусловленности , характеризующее в этом случае близость матрицы к вырожденной (сингулярной), для которой 
.
Существуют два основных класса методов для решения СЛАУ – прямые и итерационные. Прямые методы характеризуются тем, что при абсолютной точности вычислений (на гипотетической бесконечноразрядной ЭВМ) точное решение СЛАУ может быть получено с помощью конечного числа арифметических операций. Итерационные методы характеризуются тем, что даже при абсолютной точности вычислений за конечное число арифметических операций может быть получено лишь приближенное решение системы, хотя возможно и как угодно близкое к точному. Однако при реальных вычислениях на ЭВМ указанное различие теряет свой смысл, и для многих задач итерационные методы оказываются более предпочтительными, чем прямые в силу отсутствия накопления ошибок для сходящегося процесса и возможности приблизиться к решению с заданной точностью.
Рассмотрим сначала прямые методы. Наиболее известным является метод Гаусса, поскольку другие методы являются, как правило, его модификацией.
|
|
|
