 |
Условие выхода из вычислительного процесса по заданной точности в методах простой итерации
|
|
|
|
Формула (3.1) выхода из процесса итераций не всегда пригодна для практического использования. Она, например, не выполняется, если функция имеет корень в точке локального минимума. Кроме того, если алгоритм вычисления функции является плохо обусловленным (см.), относительная ошибка результата вычисления функции возле её корня может значительно превосходить машинную константу 
, а также желаемую точность определения корня. В этом случае критерий (3.1) не обеспечивает остановку итерационного процесса при достижении заданной величины 
. Заметим при этом, что в тех методах, в которых выбор текущего интервала основан на вычислении знакопеременности функции на его концах (метод дихотомии, метод хорд и т.п.), применение другого критерия не уменьшает уже возникшую в такой ситуации ошибку, а приводит лишь к выходу из процесса вычислений.
Покажем практический способ выхода из процесса итераций гарантирующий достижение заданной точности вычислений в общем случае простой итерации со знаменателем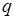 
. Считается, что корень на 
-ой итерации вычислен с точностью , если 
. Контролю же в процессе вычислений поддаётся величина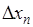 
. Установив связь между этими величинами, мы получим возможность проводить вычисления с заданной точностью. Заметим, что 
при 
. Далее, учитывая неравенство треугольника и (3.4.2)
При получаем
Таким образом, требование
(3.5.1)
обеспечивает заданную точность вычислений .
Пример и задание для практических занятий
Пример. Найти методом хорд, касательных и простой итерации корни уравнения:
, К =20, L =10. (3.6.1)
Каждый корень искать одним из предложенных методов. Для этого вначале необходимо отделить корни и выбрать метод решения. Рекомендуемый план решения приводится ниже:
|
|
|
1) Находятся первая и вторая производные:
, 
.
Очевидно, что корни (если они существуют) расположены левее, между и правее точек экстремума функции
.
Выбираются три интервала [ a, b ] и проверяется условие (3.1) на каждом интервале.
2) Для метода простых итераций уравнение преобразуется к итерационному виду: 
и выбирается интервал [a ,b ]= [3 ,5 ], на котором проверяется выполнение условия (3.1). В качестве начального значения выбирается 
, тогда по (3.1.3) получается 
, 
.
3) Для метода хорд выбирается интервал [a ,b ]= [-3, 3] и проверяется (3.1) 
, неподвижной точки на этом интервале не существует, поэтому каждый раз находится новый интервал из условия (3.1), в результате, применяя (3.2.1) получим два последовательных приближенных значения корня: 
, 
.
4) Для метода касательных выбирается интервал [a ,b ]= [-3 ,- 5] и проверяется выполнение условия (3.1) 
, выбирается начальная точка из условия (3.2.2): 
. По формуле (3.3.1) проводятся две итерации: 
, 
.
Варианты для практических и лабораторных занятий приведены в табл.4.1. Для лабораторных занятий следует графически локализовать корни, затем уточнить корни заданными методами с точностью 
, вычислить значение функции в каждом найденном корне.
Таблица 4.1
| № | ||||||||||||||||
| К | ||||||||||||||||
| L |
Численное интегрирование
Цель – приближенно вычислить определенный интеграл: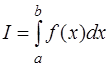 
на [ a,b ].
По теореме Ньютона – Лейбница он равен разности верхнего и нижнего пределов первообразной 
(
) функции. Но для табличных функций их первообразная не существует и даже для известных 
не всегда представима в виде комбинаций элементарных функций. Интеграл геометрически равен площади криволинейной трапеции.
|
|
|
В численных методах интеграл ищется в виде квадратуры: 
. Необходимо найти оптимальным образом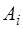 
и 
. Обычно коэффициенты подбираются так, чтобы квадратура давала точное значение для полинома максимально возможной степени.
Метод Ньютона – Котеса
Предполагается, что значения аргументов известны и расположены равномерно. Требуется найти коэффициенты А.
Рассмотрим интервал: 
, 
.
На интервале заменим интерполяционным полиномом Лагранжа (2.1.1), подставляя в него переменную q, равную:
.
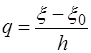
, получим 
,
где штрих означает отсутствие в произведении сомножителя с j=i
коэффициенты Аi равны:
, (4.1.1)
где 
не зависящие от интервала [ a,b ] – коэффициенты Котеса.
В дальнейшем рассматривается равномерная сетка узлов с шагом h.
Метод прямоугольников.
Степень полинома n = 0 
. Коэффициент Котеса (4.1.1) при n = 0 (вычисляется как предельный переход при 
) равен 1.Интервал 
неопределен, т.к. есть только одна точка - 
. Геометрически это обозначает, что f(x) заменяется на интервале каким-то значением ординаты. Если интервал [ a,b ] велик, то его разбивают точками на n интервалов и на каждом применяют метод прямоугольников. Для первого интервала приближенное значение интеграла равно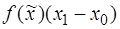 
, где 
.
В качестве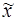 
обычно применяют:
- метод левых прямоугольников;
- метод правых прямоугольников.
На [ 
] повторяют ту же процедуру и результат суммируют
, 
. (4.2.1)
Погрешность метода на интервале длиной h равна: 
дифференцируя по h, получим: 
, 
. После интегрирования по h: 
. Абсолютная погрешность на n интервалах суммируется. В результате, учитывая, что 
получим: 
, где 
.
Метод трапеций
На частичном интервале функция заменяется линейной, т.е. n= 1. 
, 
. На интервале 
, заменяя f(x) на P1(x), получим для равноотстоящих узлов: 
. То есть, площадь криволинейной трапеции заменена площадью прямоугольной трапеции.
Суммируя по всем интервалам, приходим к выражению: 
, в котором внутренние ординаты встречается дважды. Окончательно получим:
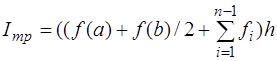. (4.3.1)
Между методом трапеций и методом прямоугольников существует простая связь:
(4.3.2)
Для оценки погрешности продифференцируем соотношение для R дважды по 
:
,
, 
.
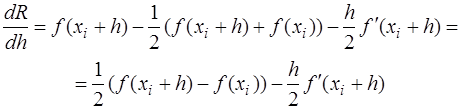Интегрируя 
дважды с заменой 
на среднее значение, приходим к выражению:
|
|
|
.
Погрешность на интервале интегрирования есть сумма погрешности на каждом частичном интервале, в результате получим: 
.
|
|
|
