 |
Прямые методы решения СЛАУ
|
|
|
|
Количество операций для решения системы 
. Матрица 
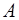либо неявно обращается, либо представляется в виде произведения матриц удобных для обращения.
В первом случае матрица 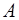последовательно преобразуется с помощью элементарных (эквивалентных) преобразований:
1. Перестановка столбцов и строк.
2. Умножение столбцов и строк на число.
3. Прибавление к строке (столбцу) другой строки, умноженной на число.
Каждое элементарное преобразование можно представить в виде матрицы 
, в результате последовательного умножения 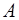на , она преобразуется в единичную матрицу:
Метод Гаусса (Метод исключений)
Формально, метод Гаусса основан на последовательном применении матриц
; 
; 
(5.2.1.1)
Пример для матрицы (3 
3):
Действие матрицы 
преобразуют элементы 
-го столбца матрицы 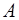ниже диагонали в нулевые (т.е. исключают их).
Вычислительная схема метода Гаусса
В каждом уравнении выделяется ведущий элемент, на который производится деление; пусть это будет 
. Делим первое уравнение на :
Все остальные элементы преобразуются по схеме:
(5.2.2.1)
На втором шаге ведущим элементом выбирается 
, на него делится вторая строка, а все остальные элементы преобразуются по формуле:
(5.2.2.2)
Элементы во втором столбце с 
2 становятся равны 0. В результате таких преобразований, мы приходим к верхней треугольной матрице с единичной диагональю:
Преобразование к верхней треугольной матрице называется прямым ходом.
Далее следует обратный ход: начиная с 
, последовательно вычисляются компоненты вектора:
; 
;
, 
. (5.2.2.3)
В машинных расчетах в качестве ведущего элемента обычно выбирается максимальный элемент 
- го столбца с 
или строки 
с 
.
|
|
|
Эта строка (или столбец) переставляются на место 
- ой строки (столбца). Такой выбор уменьшает ошибки округления. При ручных расчетах элементы матрицы записываются вместе с элементами вектора 
в расширенную матрицу:
далее из соображений удобства выбирают ведущий элемент, а преобразование остальных элементов на одном шаге прямого хода метода Гаусса проводят по правилу прямоугольника. В матрице выделяется прямоугольник, на главной диагонали которого расположены ведущий и преобразуемый элементы.
| i | … | t | … | |
| i | 
| … | 
| … |
| … | … | … | … | … |
| k | 
| … | 
| … |
| … | … | … | … | … |
Пусть 
- ведущий элемент, тогда
. (5.2.2.4)
Из преобразуемого элемента вычитается произведение элементов, стоящих на побочной диагонали, деленное на ведущий элемент.
Ортогонализация матриц
Матрица называется ортогональной, если 
, 
- диагональная матрица, т.е. в ней отличны от нуля только диагональные элементы, если 
, то 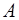- ортонормированная матрица. Любая неособенная матрица 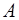может быть представлена в виде: 
, 
- ортогональная, а 
– верхняя треугольная матрица с единичной диагональю.
Рассмотрим матрицу А, как набор вектор – столбцов 
, 
- вектора - линейно независимы, т.к. 
. Выберем первый столбец матрицы - 
, равным 
; 
.
Запишем 
, условие ортогональности R 
позволяет получить 
:
, 
,
следовательно, известен и вектор 
. Аналогичным образом представляется и 
, где
, 
.
В общем случае получим выражения:
, 
. (5.2.3.1)
Покажем, что 
- элементы матрицы Т. Действительно:
, или иначе:
Решение системы уравнений методом ортогонализации
Оптимальной является следующая схема, основанная на свойствах вектора 
. Запишем систему 
в виде: 
Из структуры векторов следует, что 
, (i <j).
Умножаем систему слева на 
: 
,
в уравнении остается одно слагаемое: 
.
;
Полученную систему умножим на 
, находим 
и вычисляем 
и т.д.
; 
. (5.2.4.1)
|
|
|
Итерационные методы решения СЛАУ
Метод простой итерации
Многие итерационные методы могут быть сведены к процессу простой итерации. При этом исходное уравнение тем или иным способом должно быть сведено к уравнению
(5.3.1.1)
Здесь 
- неизвестный вектор, 
- заданный вектор правой части, 
- заданная матрица коэффициентов (оператор). Например, если задана СЛАУ (5.1), то непосредственно принимая
, (5.3.1.2)
где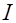 
- единичная матрица, приходим к (5.3.1.1).
Процесс простой итерации строится следующим образом:
, 
(5.3.1.3)
В качестве начального приближения 
можно принять 
.
Заметим, что переход от (5.1) к (5.3.1.1) может быть выполнен не единственным способом, что приводит к различным модификациям метода простой итерации. Так, метод (5.3.1.3) с преобразованием (5.3.1.2) известен в литературе как метод Ричардсона. Другие методы простой итерации будут рассмотрены в разделе 5.3.2.
Процесс простой итерации может быть эквивалентно записан также в виде ряда по степеням оператора , т.е., в виде, так называемого, ряда Неймана
(5.3.1.4)
Если матрица постоянна (не зависит от номера итерации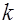 
), то такой итерационный процесс называется стационарным.
Пусть 
- «гипотетическое» точное решение, строго удовлетворяющее 
, а 
- ошибка на 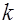-м шаге. Подставляя в формулу простой итерации получаем для соотношения ошибок на 
и 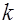-м шаге 
. Для нормы ошибки: 
.
Отсюда следует достаточное условие сходимости процесса простой итерации: 
.
Действительно, тогда
Оператор с 
называется сжимающим, а процесс (5.3.1.2), (5.3.1.3) для него сходящимся, т.к. ошибка убывает с каждым шагом, независимо от её начальной величины.
Спектральным радиусом матрицы (конечномерного оператора) называется 
, где 
- собственные числа оператора (см. 5.4).
Для любой нормы справедливо соотношение 
Доказывается, что необходимым и достаточным условием сходимости процесса простой итерации (5.3.1.3) является
< 1, (5.3.1.5)
при этом итерации сходятся не хуже геометрической прогрессии со знаменателем 
.
Условие (5.3.1.5) является, как правило, сильным ограничением при непосредственном применении метода (5.3.1.2), (5.3.1.3) к заданной СЛАУ. Выбор нового оператора 
с другим спектром при эквивалентности исходной системе (5.1) может значительно расширить область сходимости процесса простой итерации с его участием:
|
|
|
, (5.3.1.6)
В качестве условия выхода из вычислительного процесса по достижении заданной точности решения 
, аналогично (3.5.1), можно принять: 
, где 
спектральный радиус или какая-либо оценка другой нормы .
|
|
|
