 |
Численное решение начально-краевых задач для дифференциальных уравнений в частных производных
|
|
|
|
Рассматриваются простейшие уравнения математической физики гиперболического, параболического и эллиптического типов с начально-краевыми условиями для дифференциальных уравнений в частных производных (ДУЧП). Задачи такого типа возникают в физике, технике, других прикладных науках.
Для численного решения начально-краевых задач для ДУЧП используется метод конечных разностей, основанный на приближенных формулах для первой и второй производной функций. При этом начально-краевая задача заменяется на сеточные уравнения, связывающие значения искомой функции в узлах сетки.
7.1. Конечные разности.
Область решения на плоскости двух переменных, например  , разбивается на дискретную сетку из узлов
, разбивается на дискретную сетку из узлов 
 ,
,  подмножества целых чисел. Например, в прямоугольнике
подмножества целых чисел. Например, в прямоугольнике  узлы сетки:
узлы сетки: 

 , (7.1.1)
, (7.1.1)
где  шаги сетки по координатам
шаги сетки по координатам  и
и 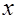 соответственно,
соответственно, 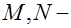 целые числа.
целые числа.
Неизвестная функция  , участвующая в краевой задаче, заменяется искомой сеточной функцией
, участвующая в краевой задаче, заменяется искомой сеточной функцией  на узлах сетки. Частные производные по координатам заменяются соответствующими конечными разностями, которые могут быть различного порядка точности по шагу сетки вдоль координаты. Пусть
на узлах сетки. Частные производные по координатам заменяются соответствующими конечными разностями, которые могут быть различного порядка точности по шагу сетки вдоль координаты. Пусть  шаг сетки вдоль рассматриваемой координаты,
шаг сетки вдоль рассматриваемой координаты,  значение функции в рассматриваемой точке
значение функции в рассматриваемой точке 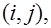
 последующие и предыдущие значения сеточной функции по данной координате. Тогда первая производная по этой координате может быть заменена правой или левой конечной разностью порядка
последующие и предыдущие значения сеточной функции по данной координате. Тогда первая производная по этой координате может быть заменена правой или левой конечной разностью порядка  :
: 
 (7.1.2)
(7.1.2)
или центральной конечной разностью порядка  :
:  (7.1.3)
(7.1.3)
Можно записать также для первой производной конечную разность порядка  :
: 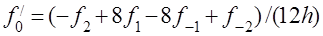
Центральные конечные разности для второй производной порядка  и
и  выглядят следующим образом:
выглядят следующим образом:  (7.1.4)
(7.1.4) 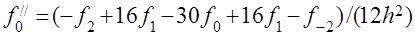
Например, для первой производной по времени можно принять правую конечную разность порядка  :
:  , а для второй производной по координате
, а для второй производной по координате 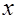 центральную конечную разность порядка
центральную конечную разность порядка  :
: 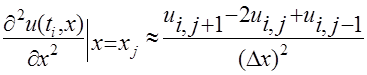
|
|
|
7.2. Гиперболическиеуравнения
В качестве примера гиперболического уравнения рассматри-вается волновое уравнение колебаний эластичной струны 
 ,
,  (7.2.1) с граничными условиями (закрепление струны на концах)
(7.2.1) с граничными условиями (закрепление струны на концах)  ,
, 

 (7.2.2) и начальными условиями первого рода для функции
(7.2.2) и начальными условиями первого рода для функции  (отклонение от положения равновесия) и второго рода для её производной (скорости отклонения)
(отклонение от положения равновесия) и второго рода для её производной (скорости отклонения)
 ,
,  для
для  (7.2.3)
(7.2.3)
На сетке (7.1.1) сеточная функция  удовлетворяет следующим соотношениям, следующим из (7.2.1) и (7.1.4)
удовлетворяет следующим соотношениям, следующим из (7.2.1) и (7.1.4) 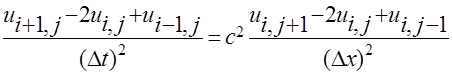
Обозначим 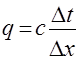 . После небольших преобразований получаем явное выражение для значения сеточной функции на
. После небольших преобразований получаем явное выражение для значения сеточной функции на 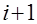 слое по времени через её значения на
слое по времени через её значения на  и
и  слоях:
слоях:
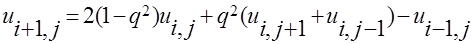 (7.2.4) для
(7.2.4) для 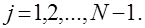
Сеточный шаблон вычислений по формуле (7.2.4) является пятиточечным, т.к. связывает между собой пять соседних узлов сетки вокруг т.  , включая её. Для того, чтобы вычисления по формуле (7.2.4) были устойчивы, необходимо выполнение соотношения
, включая её. Для того, чтобы вычисления по формуле (7.2.4) были устойчивы, необходимо выполнение соотношения  . Таким образом, условия устойчивости вычислений по явной схеме (7.2.4) накладывают ограничения на шаг по времени при заданном шаге по пространственной координате.
. Таким образом, условия устойчивости вычислений по явной схеме (7.2.4) накладывают ограничения на шаг по времени при заданном шаге по пространственной координате.
Для определения значений сеточной функции на двух начальных слоях 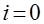 и
и  используем заданные начальные условия (7.2.2), (7.2.3) и правую конечную разность порядка
используем заданные начальные условия (7.2.2), (7.2.3) и правую конечную разность порядка  для аппроксимации первой производной в начальной точке. Использование конечной разности первого порядка точности вносит на начальном этапе ошибку большую, чем при аппроксимации уравнения во внутренних точках. В результате получаем для значений на слоях
для аппроксимации первой производной в начальной точке. Использование конечной разности первого порядка точности вносит на начальном этапе ошибку большую, чем при аппроксимации уравнения во внутренних точках. В результате получаем для значений на слоях 
 ,
, 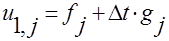 (7.2.5)
(7.2.5)
На рис. 1 показан полупериод колебаний струны рассчитанный по формулам (7.2.4), (7.2.5) при следующих исходных данных, граничных и начальных условиях: 
 ,
,  ,
,  ,
,  ,
,  ,
,  . Шаги сетки по пространственной координате и по времени
. Шаги сетки по пространственной координате и по времени  ,
, 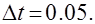
Число шагов по  и по
и по 
 соответственно
соответственно 
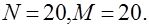

|
|
|



рис.1.
7.3. Параболическиеуравнения
Данный тип уравнений рассмотрим на примере одномерного нестационарного уравнения теплопроводности (7.3.1) с граничными (7.3.2) и начальными условиями (7.3.3), описывающего процесс установления температуры в изолированном стержне, имеющем на концах постоянную температуру  и
и  и заданное начальное распределение температуры вдоль стержня
и заданное начальное распределение температуры вдоль стержня 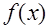 :
: 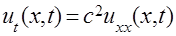
 ,
, 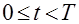 (7.3.1)
(7.3.1)
 ,
,  ,
,  (7.3.2)
(7.3.2)

 (7.3.3)
(7.3.3)
Для аппроксимации уравнения (7.3.1) используем конечные разности (7.1.2) и (7.1.4)

Обозначим 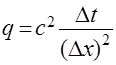 . После преобразований получаем явную четырехточечную сеточную схему, в которой значение функции на
. После преобразований получаем явную четырехточечную сеточную схему, в которой значение функции на 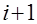 слое по времени выражается через три соседних значения на нижнем,
слое по времени выражается через три соседних значения на нижнем,  -ом слое:
-ом слое:
 (7.3.4)
(7.3.4)
Формула (7.3.4) позволяет последовательно найти все значения сеточной функции, начиная со слоя 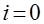 , на котором заданы начальные условия (7.3.3). Однако вычисления по этой формуле устойчивы только в том случае, если выполняется условие
, на котором заданы начальные условия (7.3.3). Однако вычисления по этой формуле устойчивы только в том случае, если выполняется условие 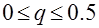 . Это накладывает жесткие ограничения на шаг сетки по времени, обязывая выбирать этот шаг намного меньшим, чем шаг по пространственной координате, что существенно увеличивает время расчета и ограничивает применимость явной схемы.
. Это накладывает жесткие ограничения на шаг сетки по времени, обязывая выбирать этот шаг намного меньшим, чем шаг по пространственной координате, что существенно увеличивает время расчета и ограничивает применимость явной схемы.
Для аппроксимации уравнения (7.3.1) может быть использована левая конечная разность (7.1.2)
 , что приводит к неявной четырёхточечной разностной схеме
, что приводит к неявной четырёхточечной разностной схеме 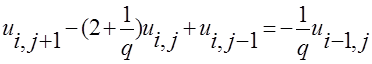 , (7.3.5) которая устойчива при любых соотношениях шагов сетки.
, (7.3.5) которая устойчива при любых соотношениях шагов сетки.
Из (7.3.5) следует, что для каждого слоя  по времени значения неизвестной сеточной функции
по времени значения неизвестной сеточной функции  ,
,  связаны СЛАУ с трехдиагональной матрицей. В этой матрице на главной диагонали находится значение
связаны СЛАУ с трехдиагональной матрицей. В этой матрице на главной диагонали находится значение  , а на двух соседних диагоналях -
, а на двух соседних диагоналях - 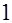 . Значение на главной диагонали близко к
. Значение на главной диагонали близко к  , т.к. значение
, т.к. значение  , как правило,
, как правило,  . Вектор в правой части (7.3.5)(при постоянном значении
. Вектор в правой части (7.3.5)(при постоянном значении  ) известен из вычислений на предыдущем шаге по времени и входит в правую часть СЛАУ.
) известен из вычислений на предыдущем шаге по времени и входит в правую часть СЛАУ.
Последовательно решая СЛАУ (7.3.5), начиная со слоя  , можно вычислить сеточную функцию во всей области решения. Система (7.3.5) может быть решена как стандартным методом (т.к. порядок системы не слишком велик -
, можно вычислить сеточную функцию во всей области решения. Система (7.3.5) может быть решена как стандартным методом (т.к. порядок системы не слишком велик -  ), так и специальными методами применяемыми для решения систем с трехдиагональными матрицами, например, методом прогонки [2].
), так и специальными методами применяемыми для решения систем с трехдиагональными матрицами, например, методом прогонки [2].
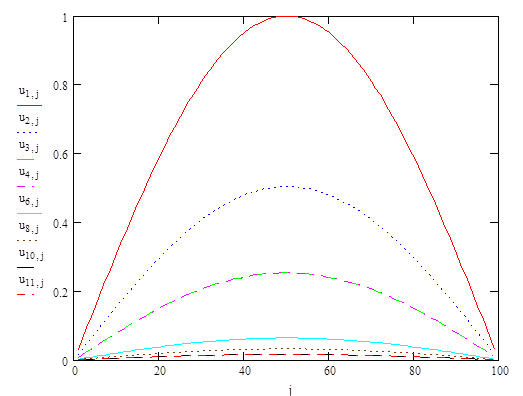
рис.2
На рис.2 представлен расчет установления температуры в стержне, проведенный по неявной схеме (7.3.5), при следующих начальных и граничных условиях:  ,
,  ;
;  ,
,  ,
,  ;
;  ,
,  . Шаги сетки по времени и по пространственной координате
. Шаги сетки по времени и по пространственной координате  ,
,  . При данном значении
. При данном значении  расчеты по явной схеме (7.3.4) были бы невозможны из-за большой неустойчивости. Число шагов по
расчеты по явной схеме (7.3.4) были бы невозможны из-за большой неустойчивости. Число шагов по  и по
и по 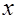 соответственно M=10, N=100.
соответственно M=10, N=100.
|
|
|
7.4. Уравнения эллиптическоготипа
Двумерные краевые задачи для уравнений данного типа рассмотрим на примере уравнений Лапласа, Пуассона и Гельмгольца. Обозначим, как обычно, оператор Лапласа 
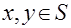
Тогда указанные уравнения имеют вид: 1.Уравнение Лапласа  2.Уравнение Пуассона
2.Уравнение Пуассона  3.Уравнение Гельмгольца
3.Уравнение Гельмгольца 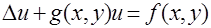
Граничные условия задаются на границе области  :
:  ,в частности, на границе прямоугольника
,в частности, на границе прямоугольника  :
:  ,
,  ,
,  ,
, 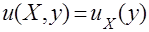
|
|
|


