 |
Разностная схема уравнений
|
|
|
|
Разностную схему рассмотрим на примере уравнения Пуассона в прямоугольнике, используя для аппроксимации второй производной конечные разности второго порядка точности (7.1.4). Вводя сетку 
, получаем 
,
или, введя обозначение 
, получаем пятиточечную разностную схему для внутренних узлов прямоугольника 
(7.4.1)
Данная неявная схема охватывает все внутренние точки области 
, их количество 
. Таково же число уравнений и неизвестных в СЛАУ, построенной на основе (7.4.1).
|
Пусть для простоты 
для всех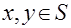 
, т.е. 
для всех внутренних точек 
, 
, а граничные условия таковы: внизу 
, слева и справа 
, 
и только наверху задана отличная от нуля функция 
. Зададим 
, 
. Тогда 
, а число внутренних точек и уравнений 
. Матрица СЛАУ для данной задачи задается по следующему закону (на языке пакета Mathcad):
Здесь 
, 
- это индексы матрицы 
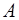, они связаны с другими, ранее введенными индексами 
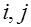для узлов сетки. Сеточная функция 
, 
, 
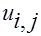выражается через найденный в результате решения СЛАУ вектор решения 
, 
следующим образом: 
.
Пятидиагональная матрица 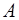имеет следующее строение:
Вектор правой части СЛАУ 
задается в данной задаче по закону:
,
где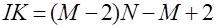 
- число, определяющее в индексах вектора решения начало последнего слоя внутренних узлов по оси 
, на которых учитывается заданное граничное условие. Заданная функция из уравнения, в данной задаче являющаяся константой,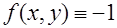 
, входит в правую часть СЛАУ в виде слагаемого 
. Значения вектора правой части в данной задаче:
На рис.3 показано распределение функции решения аналогичной краевой задачи в двумерной области при порядке СЛАУ 
. Решение получено комбинированным методом Зейделя-ОСП при оптимальном параметре 
за 
итераций с относительной точностью решения в 
. Обычный метод Зейделя сходится здесь лишь за 
итераций и сопоставим по времени решения с прямым методом. Еще большее число требуемых итераций показывают в данной задаче метод ОСП с матрицей (1.2) - 
.
|
|
|
Отметим, что матрица задачи при 
и заданном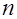 
постоянна и не зависит от краевых условий и источников 
, которые входят в правую часть СЛАУ. Соответственно задачи с различными краевыми условиями и источниками могут решаться с тем же самым оптимальным параметром, найденным один раз для данной сетки.
рис.3
Лабораторные задания к теме «Численное решение уравнений в частных производных»
Лабораторные работы по теме могут быть выполнены с помощью математических пакетов программ Mathcad или Matlab. В результате работы должна быть представлена искомая сеточная функция в виде матрицы значений в узлах сетки либо в виде послойного по времени распределения значений сеточных векторов. Следует также привести графическое представление результатов.
Гиперболические уравнения
Варианты заданий для одномерного волнового уравнения с граничными и начальными условиями (см. 7.2).
| № п/п | 
| 
| 
| 
| 
| 
| 
| 
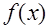
| Метод 
|
| 1.1 | 
| 
| 0.1, 0.05 | ||||||
| 1.2 | 
|
| 0.1, 0.05 | ||||||
| 1.3 |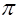 
| 
|
| 0.1, 0.05 | |||||
| 1.4 | 
|
| 0.1, 0.05 | ||||||
| 1.5 |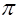
| 
|
| 0.1, 0.05 | |||||
| 1.6 | 
|
| 0.1, 0.05 | ||||||
| 1.7 |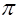
| 
|
| 0.1, 0.05 | |||||
| 1.8 |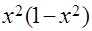 
|
| 0.1, 0.05 | ||||||
| 1.9 |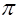
| 
|
| 0.1, 0.05 | |||||
| 1.10 | 
|
| 0.1, 0.05 |
Параболические уравнения
Варианты заданий для одномерного уравнения теплопроводности с граничными и начальными условиями (см. 7.3).
| № п/п |
|
|
|
|
|
|
|
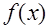
| Метод
|
| 2.1 | 0.1 |
|
| 0.01 | |||||
| 2.2 |
|
| 0.01 | ||||||
| 2.3 | 0.1 |
|
| 0.01 | |||||
| 2.4 |
|
| 0.01 | ||||||
 2.5
|
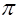
| 0.1 |
|
| 0.01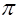
| ||||
| 2.6 |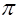
|
|
| 0.01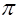
| |||||
| 2.7 |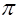
| 0.1 |
|
| 0.01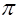
| ||||
| 2.8 |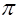
|
|
| 0.01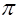
| |||||
| 2.9 | 0.1 |
|
| 0.01 | |||||
| 2.10 |
|
| 0.01 | ||||||
| 2.11 |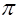
| 0.1 |
|
| 0.01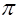
| ||||
| 2.12 |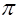
|
|
| 0.01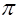
|
|
|
|
Методы: 1- явный; 2 - неявный, сведением к СЛАУ и последующим решением стандартным методом. Сравнить со строгим решением.
Эллиптические уравнения
Решить заданную краевую задачу методом сеток, сведением её к СЛАУ и последующим решением прямым (стандартным) и итерационным (Зейделя-ОСП) методами. Сравнить с существующим строгим решением.
Варианты заданий для краевой задачи с уравнениями эллиптического типа (см. 7.4).
| № п/п | Уравнение 
|
| 
| 
| 
| 
| 
| 
|
| |
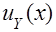
| 3.1 | 
| 0.2, 0.1 | - | |||||||
| 3.2 | 
| 
| 
| 
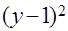
| 0.2, 0.1 | -1 | ||||
| 3.3 | 
| 0.2, 0.1 | - | |||||||
| 3.4 | 
| 0.2, 0.1 | 0,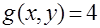 
| |||||||
| 3.5 |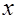 
|
| 0.2, 0.1 | - | ||||||
| 3.6 | 
|
|
| 
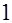
| 0.2, 0.1 |
| ||||
| 3.7 | 0.5, 0.25 | - | ||||||||
| 3.8 |
| 0.2, 0.1 | - 2 | |||||||
| 3.9 | 0.25,0.1 | - | ||||||||
| 3. |
| 
| 
| 
| 0.2, 0.1 | |||||
уравнения: 1-Лапласа, 2-Пуассона, 3-Гельмгольца
Литература
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2001. – 632с.
2. Мэтьюз Д.Г., Финк К.Д., Численные методы. Использование MATLAB, 3-е издание,: Пер. с англ. – М.: Изд. «Вильямс», 2001. – 720 с.
3. А.Б.Самохин, А.С.Самохина. Численные методы и программирование на Фортране для персонального компьютера.- М.: Радио и связь, 1996. – 224 с.
4. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970. – 644с.
5. Вержбицкий В.М., Численные методы (Математический анализ и обыкновенные дифференциальные уравнения) – М.: Высшая школа, 2001.– 382с.
6. Заварыкин В.М., Житомирский В.Г., Лапчин М.П. Численные методы. – М.: Просвещение, 1991. – 176с.
Содержание
Введение. 3
1. Абсолютная и относительная погрешности. 3
1.1. Число верных знаков приближенного числа. 4
1.2. Погрешность функций. 5
1.3. Погрешность простейших функций двух переменных. 5
1.4. Примеры и задания. 6
|
|
|
2. Приближение функций. 10
2.2. Интерполяционный полином Лагранжа. 11
2.3. Интерполяционный полином Ньютона. 12
2.3. Примеры и задания для практических занятий. 15
3. Численные методы решений трансцендентных и алгебраических уравнений 18
3.1. Метод простой итерации для решения нелинейных и трансцендентных уравнений. 19
3.2. Метод хорд и секущих. 20
3.3. Метод касательных. 21
3.4. Скорость сходимости итерационных методов. 22
3.5. Пример и задание для практических занятий. 24
4. Численное интегрирование. 25
4.1. Метод Ньютона – Котеса. 25
4.2. Метод прямоугольников. 26
4.3. Метод трапеций. 27
4.4. Метод парабол. (Метод Симпсона) 28
4.5. Квадратурные формулы Гаусса. 29
4.6. Задание для практических занятий. 31
5. Численные методы линейной алгебры.. 32
5.1. Численное решение СЛАУ.. 32
5.2. Прямые методы решения СЛАУ.. 35
5.2.1. Метод Гаусса (Метод исключений) 36
5.2.2. Вычислительная схема метода Гаусса. 37
5.2.3. Ортогонализация матриц. 39
5.2.4. Решение системы уравнений методом ортогонализации. 40
5.3. Итерационные методы решения СЛАУ.. 41
5.3.1. Метод простой итерации. 41
5.3.2. Метод Якоби и метод Зейделя. 43
5.3.3. Метод оптимального спектрального параметра (ОСП) для простой итерации. 46
5.4. Нахождение собственных векторов и собственных значений матриц 52
5.5. Примеры и задания к теме. 53
5.5.1. Прямые методы решения СЛАУ.. 53
5.5.2. Итерационные методы решения СЛАУ.. 57
5.5.3. Нахождение собственных значений и векторов. 61
6. Численные методы решения обыкновенных дифференциальных уравнений 62
6.1. Метод разложения в ряд Тейлора. 63
6.2. Общая схема метода Рунге - Кутта. 63
6.3 Методы Рунге-Кутта низших порядков. 64
6.3.1 Метод Эйлера. 64
6.3.2. Метод трапеций и прямоугольника. 65
6.4. Методы Рунге-Кутта высших порядков. 65
6.5. Задание к теме и пример решения ОДУ.. 67
7. Численное решение начально-краевых задач для дифференциальных уравнений в частных производных. 68
7.1. Конечные разности. 69
7.2. Гиперболическиеуравнения. 70
7.3. Параболическиеуравнения. 72
7.4. Уравнения эллиптическоготипа. 75
7.4.1. Разностная схема уравнений. 75
7.5. Лабораторные задания к теме «Численное решение уравнений в частных производных». 79
|
|
|
7.5.1. Гиперболические уравнения. 79
7.5.2. Параболические уравнения. 80
7.5.3. Эллиптические уравнения. 80
Литература. 82
Содержание. 83
|
|
|
