Метод оптимального спектрального параметра (ОСП) для простой итерации

 

Рассмотрим случай, когда спектр оператора выходит за границы единичного круга на комплексной -плоскости собственных чисел. В этом случае ряд простой итерации (5.3.1.3) расходится.

Определим выпуклую оболочку спектра оператора как выпуклую замкнутую кривую наименьшей меры, полностью охватывающую спектр оператора на -плоскости. Доказывается, что если точка 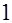находится вне выпуклой оболочки спектра, то можно построить сходящийся ряд простой итерации с новым

 

 

Рис.1

 

оператором 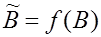. Дадим конструктивный способ построения такого сходящегося ряда. Примем:

, , (5.3.3.1)

 

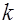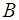где - комплексный параметр. При исходные уравнения (5.3.1.1) с операторами и эквивалентны. Выбором 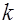попробуем добиться сходимости ряда (5.3.1.6).

Пусть - один из множества кругов радиуса , полностью охватывающих спектр оператора , и пусть при этом точка (Рис.1). Очевидно, что включает в себя выпуклую оболочку спектра. Вектор из начала в центр этого круга обозначим . При дробно-линейном преобразовании (5.3.3.1) с круг переходит в круг с центром в точке 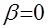и радиусом . Если , то ряд (5.3.1.6) сходится.

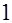Найдем минимум значения . Пусть круг «виден» из точки под углом . Пусть вектор из центра круга в точку касания луча из т.1 и круга. Из рис. 1 очевидно, что и, следовательно, .

Таким образом, если такой круг, что точка и «видимый» из точки под наименьшим углом , то комплексное расстояние до центра этого круга есть оптимальный параметр для сходимости (5.3.1.6), а скорость сходимости ряда (5.3.1.6) не хуже, чем у геометрической прогрессии со знаменателем .

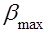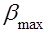Пусть для спектра известны оценки для , -минимального и максимального по модулю собственного числа (или нижней и верхней границы расстояния от т. 0 до области расположения спектра в случае непрерывного спектрального множества). Тогда, если весь спектр оператора размещается в круге , натянутом на точки , как на концевые точки диаметра и точка , для оптимального параметра верна простая приближенная формула

(5.3.3.2)

Если граница круга принадлежит спектру, то формула (5.3.3.2) точная. Точная она также и в случае вещественного спектра. Формулу (5.3.3.2) можно улучшить, учитывая более точную конфигурацию спектральной области, например, если область расположения спектра – прямая линия. С помощью формулы (5.3.3.2) во многих случаях можно найти значение близкое к оптимальному параметру в условиях неполного знания свойств спектра, но при известных минимальных и максимальных по модулю собственных числах.

Сходимость каждого из рассмотренных методов простой итерации зависит от конкретного вида исходной матрицы, а точнее, от свойств её спектра. Можно привести примеры матриц, для которых сходится только один из рассмотренных методов, однако комбинация метода простой итерации, Зейделя или Якоби с методом оптимального спектрального параметра (ОСП) позволяют добиться сходимости в случаях, когда каждый из этих методов по отдельности расходится.

Рассмотрим применение метода ОСП на примерах конкретных матричных задач.

Пусть элементы матрицы при следующие: , , , . Cобственные числа матрицы (5.3.1.2) равны , и располагаются по разные стороны от точки 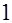на прямой, проходящей через неё. В этом случае точка 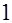принадлежит выпуклой оболочке спектра и дробно-линейным преобразованием (5.3.3.1) нельзя добиться сходимости итерационного процесса. Собственные же числа матрицы Якоби (5.3.2.3) равны 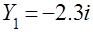, (здесь - мнимая единица) и точка 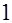находится вне выпуклой оболочки спектра. То же самое можно утверждать и о спектре оператора Зейделя. Однако, непосредственное применение метода Якоби или Зейделя не приведёт к сходящемуся ряду, т.к. и не выполняется (5.3.1.5). 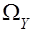Заключая спектр в круг с центром в т. приходим к сходящемуся методу Якоби – ОСП с параметром . Для метода Зейделя - ОСП оптимальный параметр приводит к быстро сходящемуся процессу. Решение СЛАУ (5.1) с правой частью и точностью достигается за 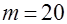итераций ряда (5.3.1.6).

Наоборот, если матрица Якоби (оператор Зейделя) имеют спектр, выпуклая оболочка которого содержит т. 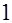, то никакие модификации этих методов не приведут к сходящемуся процессу. Применение метода ОСП непосредственно к исходной матрице в виде (1.2) может привести в этом случае к сходимости. Такова матрица с элементами 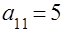, , , , 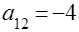для которой собственные числа матрицы (1.2) , , а собственные числа матрицы (2.3) - , . Применение методов Якоби и Зейделя и их модификаций дают расходящийся процесс, т.к. точка 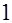принадлежит выпуклой оболочке спектра. Применение же метода ОСП к простой итерации с матрицей (5.3.1.2) дает быстро сходящийся ряд. Решение СЛАУ (5.1) с точностью достигается за итераций ряда (5.3.1.6).

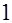Применение метода ОСП наиболее успешно в том случае, когда спектр оператора в (1.1) локализован в небольшой окрестности с центром в т. вдали от точки . Тогда применение этого метода с оптимальным параметром является самым удачным среди одношаговых стационарных методов и приводит к быстро сходящемуся ряду простой итерации. В качестве примера рассмотрим СЛАУ с матрицей , , , . В этом примере для матриц (1.2) и (2.3) имеем следующие собственные числа , и , . Значение оптимального параметра 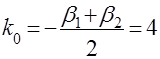переводит в данном случае точку , в которой находится весь спектр матрицы , в точку 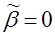, в которой находится спектр матрицы . Таким образом, скорость сходимости ряда (5.3.1.6) с матрицей (5.3.3.1), (5.3.1.2) в данном случае очень высокая, т.к. . Решение СЛАУ (1) с точностью до машинной константы достигается за итерации. Решение той же задачи методами Якоби и Зейделя требует гораздо большего количества итераций - и соответственно. Для метода Якоби применение ОСП не даст улучшения сходимости, т.к. центр спектра и так находится в точке и оптимальный параметр . Для метода же Зейделя спектр оператора (5.3.2.5) отличается от спектра матрицы (5.3.2.3) и использование метода Зейделя-ОСП с оптимальным параметром , т.е. ряда (1.6) с оператором (5.3.3.1), (5.3.2.5), приводит к уменьшению требуемого количества итераций - .

Пусть рассмотренная матрица продолжена на большую трехдиагональную матрицу с и такими же элементами, т.е. на главной диагонали чередуются значения и 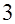, а на двух соседних соответственно 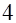и . Спектр исходной матрицы существенно трансформируется из точки в протяженную область на комплексной плоскости, но при этом значение оптимального параметра, полученного по формуле (5.3.3.2) с участием минимального и максимального по модулю собственного числа матрицы (5.3.1.2), остается неизменным . Это справедливо для любой трехдиагональной матрицы, полученной таким периодическим продолжением из малой матрицы. Однако это значение все же приближенное в силу того, что матрица не является положительно определенной и другие комплексные собственные числа выходят за пределы круга, натянутого на как на диаметр. Опытным путем для сравнительно малых матриц с значение оптимального параметра можно уточнить до 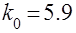и это значение остается практически неизменным для всех больших матриц такого вида. Для параметров и 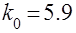и точности решения получаем соответственно число требуемых итераций и . Впечатляющий результат для данной задачи приносит метод Зейделя-ОСП. Если для обычного метода Зейделя число итераций , то с применением ОСП при число требуемых итераций снижается до !

Конечно, задача определения спектра матрицы в общем случае ничем не проще задачи решения СЛАУ прямыми методами. Однако, для ряда матриц приближенное значение оптимального параметра для метода ОСП в применении к простой итерации (5.3.1.2), (5.3.1.3) находится весьма просто через её коэффициенты. Например, для большой трехдиагональной матрицы с двумя постоянными диагоналями возле главной и с чередующимися значениями и коэффициентов на главной диагонали. Для такой матрицы в (5.1) значение оптимального параметра в (5.3.1.6) с (5.3.3.1), (5.3.1.2) равно и, если - положительно определенная матрица, то это значение точное. Это не значит, что для любой матрицы такого типа можно построить сходящийся итерационный процесс, но если можно добиться сходимости, то при таком метод сходится.

Кроме того, для физических и технических задач область локализации спектра оператора часто известна, т.к. она соответствует физически нерегулярным и резонансным решениям.

Преобразование оператора (5.3.3.1) можно использовать в условиях неполной информации об его спектре. Так, например, если известна в точности только одна граница вещественного спектра. Более определенно, пусть известно, что собственные числа находятся на интервале и значение известно точно, а для известно лишь, что . Т.к. для данного случая 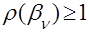, то ряд простой итерации расходится, но в силу того, что можно построить сходящийся ряд. Действительно, принимая 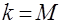, получаем сходящийся ряд простой итерации для оператора , спектр которого лежит на интервале , причем , т.е. . Можно показать также, что в условиях неопределенности данной задачи 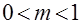лучший результат даст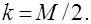

Если даже приходится детально исследовать спектр задачи для построения быстро сходящегося итерационного процесса то, однажды его построив, можно затем многократно использовать для расчетов с различными источниками - правыми частями .

Преимущества же быстро сходящихся итерационных процессов перед прямыми методами известны. Это:

· количество арифметических операций (здесь - число итераций), вместо ;

· отсутствие накопления ошибок в процессе итераций со сжимающим оператором;

· пониженные требования к оперативной памяти ЭВМ.

Особенно эти преимущества заметны для задач с большими матрицами . Решение СЛАУ с стандартным методом Mathcad на ЭВМ P-2 750Мгц занимает около 3 мин машинного времени, в то время как решение той же системы быстро сходящимся итерационным методом с требует всего около 1..2 сек.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: